Question

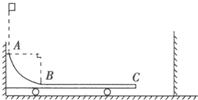
如图所示，水平光滑地面上放一质量M=3kg的小车，左侧靠在竖直墙上，小车的四分之一圆弧轨道AB是光滑的，最低点B与粗糙的水平轨道BC相切．质量m=lkg的小滑块从A点正上方距BC竖直高度h=1.8m处无初速下落，滑过圆弧轨道后沿水平方向在小车上滑动．当小车与滑块达到共同速度后，小车与右侧的竖直墙壁发生碰撞，小车立即原速率反弹，之后滑块从小车上掉下做自由落体运动，已知滑块与BC间的动摩擦因数μ=0.3，g=10m/S²，不计空气阻力，求：
（1）滑块到达小车上B点时的速度大小；
（2）滑块自B点开始到与小车速度相同时所用时间；
（3）BC的长度．

Answer 1

解（1）设物块到达B点的速度为v_B，有：mgh=

1

2

m

v

21

解得：v1=

2gh

=

2×10×1.8

m/s=6m/s
（2）以物块及小车系统为研究对象，向右的方向为正方向，根据动量守恒得：mv₁=（M+m）v₂
解得：v2=

mv1

M+m

=

1×6

3+1

m/s=1.5m/s
设滑块自B点开始到与小车速度相同时所用时间t，则：-μmg?t=mv₂-mv₁
t=

v1-v2

μg

=

6-1.5

0.3×10

s=1.5s
（3）当小车与滑块达到共同速度时，滑块的位移：x1=

v1+v2

2

?t=

6+1.5

2

×1.5m=5.625m
小车的位移：x2=

v2

2

?t=

1.5

2

×1.5m=1.125m
小车与右侧的竖直墙壁发生碰撞，小车立即原速率反弹，滑块则在小车上向右做减速运动，由于滑块从小车上掉下做自由落体运动，所以滑块的末速度是0，
该过程中小车与滑块组成的系统动量守恒，设小车的末速度是v ₃，向右的方向为正方向，得：
-Mv₂+mv₂=Mv₃+m×0
得：v3=

-Mv2+mv2

M

=

-3×1.5+1×1.5

3

m/s=-1m/s
该过程对应的时间：-μmgt′=0-mv₂
得：t′=

v2-0

μg

=

1.5

0.3×10

s=0.5s
该时间内，滑块的位移：x3=

v2+0

2

×t′=

1.5

2

×0.5m=0.375m
小车的位移：x4=

(-v2)+v3

2

?t′=

-1.5-1

2

×0.5m=-0.625m
整个的过程中小车与滑块的相对位移：△x=x₁-x₂+x₃-x₄=5.625-1.125+0.375-（-0.625）=5.5m
整个的过程中小车与滑块的相对位移即小车的BC段的长度．
答：（1）滑块到达小车上B点时的速度大小是6m/s；
（2）滑块自B点开始到与小车速度相同时所用时间是1.5s；
（3）BC的长度是5.5m．