��Ŀ����
����Ŀ��С���A������Ϊm��������µ���Ķ�Ħ������Ϊ�̣�ˮƽ��⻬���µ����˾�ˮƽ��߶�Ϊh�����Ϊ�ȣ������µ�����ˮƽ����ʱ���ڵ�O�㴦��е����ʧ���������ٶ�Ϊg�����ᵯ�ɵ�һ��������ˮƽ����M�����̶�ǽ�ϣ���һ���ɶ�ǡλ���µ��ĵ�O�㣬��ͼ��ʾ�����A���¶��ɾ�ֹ���£���
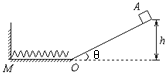
��1����黬��O��ʱ���ٶȴ�С��
��2������Ϊ���ѹ����dʱ�ĵ������ܣ�
��3�����A�����ص��µ����������߶ȣ�
���𰸡���1����黬��O��ʱ���ٶȴ�СΪ![]() ��
��
��2������Ϊ���ѹ����dʱ�ĵ�������Ϊmgh����mghcot�ȣ�
��3�����A�����ص��µ����������߶�Ϊ![]()
��������
�����������1���ɶ��ܶ�����
mgh��![]() =
=![]()
��ã�![]()
��2����ˮƽ���ϣ���е���غ㶨�ɵ�
![]()
�������Ep=mgh����mghcot��
��3��������A�ܹ����������߶�h1��
���屻���ع������ɶ��ܶ�����
��mgh1��![]() =0��
=0��![]()
��ã�![]()

 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
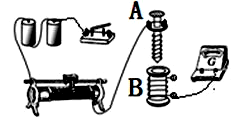
�»ƸԱ����ܾ�ϵ�д�����Ŀ����ͼ����ʾΪ�����綯��ת�����ٶȵ�ʵ��װ�ã��뾶�����Բ�ο�ֽ�̶��ڵ綯��ת���ϣ��ڵ綯���Ĵ���������ת������Բ�ο�ֽ���Ա߰�װһ����װ�˵ĵ��ʱ����
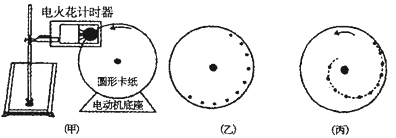
�����Ǹ�ʵ���ʵ�鲽�裺
��ʹ���ʱ����Բ�ο�ֽ�������ýӴ���
�������綯����ʹԲ�ο�ֽת��������
�۽�ͨ���ʱ���ĵ�Դ��ʹ������������
�ܹرյ綯����������ʱ�����о���ֽ�����µ�һ�κۼ�����ͼ����ʾ����д�����ٶȦصı���ʽ���������ݣ��ó��صIJ���ֵ��
��1��Ҫ�õ����ٶȦصIJ���ֵ����ȱ��һ�ֱ�Ҫ�IJ������ߣ�����________
A����� | B���α꿨�� | C��Բ�� | D�������� |
��2������ʱ�����ʱ����Ϊt����ֽ�����������µ�n���㣬д���صı���ʽ����ָ������ʽ�и����������ĺ���__________________��
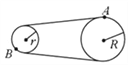
��3��Ϊ�˱����ڿ�ֽ����ת���Ĺ����г��ִ���ص����ڵ��ʱ�������汣�����ýӴ���ͬʱ�����Ի����ؽ����ʱ����Բ�ο�ֽ�뾶������ֽ�����ƶ�����ֽ�ϴ��µĵ�ķֲ����߲���һ��Բ����������һ�������ߣ���ͼ����ʾ������Ϊ��Բ����������Ӱ�죬д������_____________________