��Ŀ����
����Ŀ����ͼ��б��ֲڣ�����![]() ����б���ϣ�������һ����
����б���ϣ�������һ����![]() ��
��![]() ��б���Ķ�Ħ������
��б���Ķ�Ħ������![]() ��
��![]() ��
��![]() ֮���Ħ������Ϊ
֮���Ħ������Ϊ![]() ����ʼʱ
����ʼʱ![]() �������
�������![]() ���ڵ��м�λ���Ҳ���
���ڵ��м�λ���Ҳ���![]() ��ǰ��Ӵ������ڽ�
��ǰ��Ӵ������ڽ�![]() ������ͬʱ�ɾ�ֹ�ͷţ����մﵽƽ��ʱ
������ͬʱ�ɾ�ֹ�ͷţ����մﵽƽ��ʱ![]() ��������Ծ�ֹһ����б���»���������˵����ȷ���ǣ���
��������Ծ�ֹһ����б���»���������˵����ȷ���ǣ���
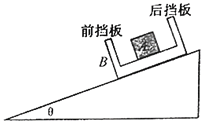
A.��![]() �����ȶ�������
�����ȶ�������![]() ������
������![]() ��ǰ����
��ǰ����
B.��![]() ������ͷſ�ʼ����
������ͷſ�ʼ����![]() ��һֱ�����
��һֱ�����![]() ��ֹ
��ֹ
C.����![]() ����ʲô��ϵ���ȶ�������
����ʲô��ϵ���ȶ�������![]() ����������
����������![]() �ĺ�
�ĺ�
D.����![]() �������
�п�������![]() �ĺ���
�ĺ���![]() һ���ȼ����»�
һ���ȼ����»�
���𰸡�AC
��������
��![]() �����ȶ�������ļ��ٶ�Ϊa�������壬����ţ�ٵڶ������У�
�����ȶ�������ļ��ٶ�Ϊa�������壬����ţ�ٵڶ������У�
![]()
��ã�![]()
�赵���Aû��������������ţ�ٵڶ������У�
![]()
��ã�![]()
��A��B������Ħ����Ϊ��
![]()
��![]() ��˵������B��A����б�����ϵĵ������ã����ȶ���A����B��ǰ����һ�������ȼ��ٶȣ���һ��ʼʱ��A�ļ��ٶȴ���B�ļ��ٶȣ���A��B��ǰ����Ӵ�ʱ�������ٶ���ȣ�
��˵������B��A����б�����ϵĵ������ã����ȶ���A����B��ǰ����һ�������ȼ��ٶȣ���һ��ʼʱ��A�ļ��ٶȴ���B�ļ��ٶȣ���A��B��ǰ����Ӵ�ʱ�������ٶ���ȣ�
��![]() ���赵���Aû��������������ţ�ٵڶ������У�
���赵���Aû��������������ţ�ٵڶ������У�
![]()
��ã�![]()
��A��B������Ħ����Ϊ��
![]()
��![]() ��˵�������Aû������������һ��ʼʱA�����B��ֹ��һ���������ȼ���ֱ���˶������Ϸ�����֪������
��˵�������Aû������������һ��ʼʱA�����B��ֹ��һ���������ȼ���ֱ���˶������Ϸ�����֪������![]() ��ʲô��ϵ���ȶ�������A����������B�ĺ壬AC��ȷ��BD����
��ʲô��ϵ���ȶ�������A����������B�ĺ壬AC��ȷ��BD����
��ѡAC��