题目内容
6. 如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,将两个小圆环固定在大圆环竖直对称轴的两侧θ=30°的位置上,一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小,在两个小圆环间绳子的中点C处挂上一个质量为M=$\sqrt{2}$m的重物,使两个小圆环间的绳子水平,然后无初速地释放重物M,设绳子与大、小圆环间的摩擦可忽略,求重物M下降的最大距离.
如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,将两个小圆环固定在大圆环竖直对称轴的两侧θ=30°的位置上,一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小,在两个小圆环间绳子的中点C处挂上一个质量为M=$\sqrt{2}$m的重物,使两个小圆环间的绳子水平,然后无初速地释放重物M,设绳子与大、小圆环间的摩擦可忽略,求重物M下降的最大距离.
分析 无初速释放重物M后,当M的速度为0时,重物M下降的距离最大.设此时重物M下落的高度为H,对两个m和M组成的系统,机械能守恒,根据机械能守恒定律即可求解.
解答 解:设重物M下降的最大距离为H,此时两物体上升的最大高度为h
对于M和两个物体m组成的系统,机械能守恒
则:△EP=-MgH+2mgh
△EK=0
又因为△EP+△EK=0
$h=\sqrt{{H^2}+{{({RSinθ})}^2}}-RSinθ$
解得:$H=\sqrt{2}R$
另一解H=0(舍去)
答:重物M下降的最大距离是$\sqrt{2}R$.
点评 本题主要考查了机械能守恒定律得应用,要知道无初速释放重物M后,当M所受合外力为0时,加速度为0,速度最大,当M的速度为0时,重物M下降的距离最大.

练习册系列答案
相关题目
16.有一家用电风扇,电风扇两端的电压为220V,工作电流为0.5A,则下列说法中,正确的是( )
| A. | 电扇线圈的电阻为440Ω | B. | 电扇线圈的电阻大于440Ω | ||
| C. | 电扇线圈的电阻小于440Ω | D. | 电风扇线圈的电阻满足欧姆定律 |
14. 荡秋千一直是小朋友们喜爱的运动项目,秋千上端吊环之间不断磨损,承受拉力逐渐减小.如图所示,一质量为m的小朋友在吊绳长为l的秋千上,如果小朋友从与吊环水平位置开始下落,运动到最低点时,吊绳突然断裂,小朋友最后落在地板上.如果吊绳的长度l可以改变,则( )
荡秋千一直是小朋友们喜爱的运动项目,秋千上端吊环之间不断磨损,承受拉力逐渐减小.如图所示,一质量为m的小朋友在吊绳长为l的秋千上,如果小朋友从与吊环水平位置开始下落,运动到最低点时,吊绳突然断裂,小朋友最后落在地板上.如果吊绳的长度l可以改变,则( )
 荡秋千一直是小朋友们喜爱的运动项目,秋千上端吊环之间不断磨损,承受拉力逐渐减小.如图所示,一质量为m的小朋友在吊绳长为l的秋千上,如果小朋友从与吊环水平位置开始下落,运动到最低点时,吊绳突然断裂,小朋友最后落在地板上.如果吊绳的长度l可以改变,则( )
荡秋千一直是小朋友们喜爱的运动项目,秋千上端吊环之间不断磨损,承受拉力逐渐减小.如图所示,一质量为m的小朋友在吊绳长为l的秋千上,如果小朋友从与吊环水平位置开始下落,运动到最低点时,吊绳突然断裂,小朋友最后落在地板上.如果吊绳的长度l可以改变,则( )| A. | 吊绳越长,小朋友在最低点越容易断裂 | |
| B. | 吊绳越短,小朋友在最低点越容易断裂 | |
| C. | 吊绳越长,小朋友落地点越远 | |
| D. | 吊绳长度是吊绳悬挂点高度的一半时,小朋友落地点最远 |
1.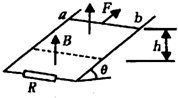 如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速上滑,则它在上滑h高度的过程中,以下说法正确的是( )
如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速上滑,则它在上滑h高度的过程中,以下说法正确的是( )
 如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速上滑,则它在上滑h高度的过程中,以下说法正确的是( )
如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速上滑,则它在上滑h高度的过程中,以下说法正确的是( )| A. | 作用在金属棒上各力的合力做功为零 | |
| B. | 恒力F做的功等于金属棒重力势能的增加 | |
| C. | 恒力F做的功等于电阻R上发出的焦耳热 | |
| D. | 金属棒克服安培力做的功等于电阻R上产生的焦耳热 |
11.下列几种情况,系统的机械能守恒的是( )
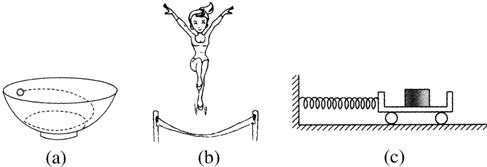

| A. | 图(a)中一颗弹丸在光滑的碗内做复杂的曲线运动 | |
| B. | 图(b)中运动员在蹦床上越跳越高 | |
| C. | 图(c)中小车上放一木块,小车的左侧有弹簧与墙壁相连.小车在左右振动时,木块相对于小车无滑动(车轮与地面摩擦不计) | |
| D. | 图(c)中如果小车振动时,木块相对小车有滑动 |
18. 如图所示在同一轨道平面内的三颗不同的人造地球卫星A、B、C,关于各物理量的关系,下列说法正确的有( )
如图所示在同一轨道平面内的三颗不同的人造地球卫星A、B、C,关于各物理量的关系,下列说法正确的有( )
 如图所示在同一轨道平面内的三颗不同的人造地球卫星A、B、C,关于各物理量的关系,下列说法正确的有( )
如图所示在同一轨道平面内的三颗不同的人造地球卫星A、B、C,关于各物理量的关系,下列说法正确的有( )| A. | 向心加速度aA>aB>aC | B. | 根据万有引力定律,FA>FB>FC | ||
| C. | 根据v=$\sqrt{gr}$可知vA<vB<vC | D. | 运动一周后,C先回到原地点 |
13.历史上第一个在实验室里比较准确地测出引力常量的科学家是( )
| A. | 哥白尼 | B. | 开普勒 | C. | 牛顿 | D. | 卡文迪许 |