题目内容
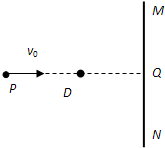 (2007?宝坻区一模)如图所示,MN为纸面内竖直放置的挡板,P、D是纸面内水平方向上的两点,两点距离PD为L,D点距挡板的距离DQ为
(2007?宝坻区一模)如图所示,MN为纸面内竖直放置的挡板,P、D是纸面内水平方向上的两点,两点距离PD为L,D点距挡板的距离DQ为| L | π |
(1)粒子在加上磁场前运动的时间t;
(2)满足题设条件的磁感应强度B的最小值及B最小时磁场维持的时间t0的值.
分析:(1)先画出粒子运动的轨迹,由图可知在加上磁场前瞬间微粒在F点(圆和PQ的切点).在t时间内微粒从P点匀速运动到F点,根据几何关系及圆周运动半径公式联立即可求解;
(2)微粒在磁场中作匀速圆周运动时,当R最大时,B最小,在微粒不飞出磁场的情况下,R最大时有:DQ=2R,微粒在磁场中做圆周运动的时间为
+n个周期,根据周期公式即可求解.
(2)微粒在磁场中作匀速圆周运动时,当R最大时,B最小,在微粒不飞出磁场的情况下,R最大时有:DQ=2R,微粒在磁场中做圆周运动的时间为
| 3 |
| 4 |
解答: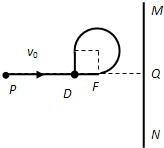 解:(1)微粒从P点至第二次通过D点的运动轨迹如图所示
解:(1)微粒从P点至第二次通过D点的运动轨迹如图所示
由图可知在加上磁场前瞬间微粒在F点(圆和PQ的切点).
在t时间内微粒从P点匀速运动到F点,t=
…①
由几何关系可知:PF=L+R… ②
又 R=
…③
由①②③式可得:t=
+
(2)微粒在磁场中作匀速圆周运动时,由②式可知:当R最大时,B最小,在微粒不飞出磁场的情况下,R最大时有:
DQ=2R,
即
=2R
可得B的最小值为:Bmin=
微粒在磁场中做圆周运动,故有t0=(n+
)T,n=0,1,2,3,
又:T=
即可得:t0=
,(n=0,1,2,3,…)
答:(1)粒子在加上磁场前运动的时间t为
+
;
(2)满足题设条件的磁感应强度B的最小值为
,B最小时磁场维持的时间t0为
,(n=0,1,2,3,…).
 解:(1)微粒从P点至第二次通过D点的运动轨迹如图所示
解:(1)微粒从P点至第二次通过D点的运动轨迹如图所示由图可知在加上磁场前瞬间微粒在F点(圆和PQ的切点).
在t时间内微粒从P点匀速运动到F点,t=
| PF |
| v0 |
由几何关系可知:PF=L+R… ②
又 R=
| mv0 |
| Bq |
由①②③式可得:t=
| L |
| v0 |
| m |
| Bq |
(2)微粒在磁场中作匀速圆周运动时,由②式可知:当R最大时,B最小,在微粒不飞出磁场的情况下,R最大时有:
DQ=2R,
即
| L |
| π |
可得B的最小值为:Bmin=
| 2πmv0 |
| qL |
微粒在磁场中做圆周运动,故有t0=(n+
| 3 |
| 4 |
又:T=
| 2πm |
| Bq |
即可得:t0=
(n+
| ||
| v0 |
答:(1)粒子在加上磁场前运动的时间t为
| L |
| v0 |
| m |
| Bq |
(2)满足题设条件的磁感应强度B的最小值为
| 2πmv0 |
| qL |
(n+
| ||
| v0 |
点评:本题是带电粒子在磁场场中运动的问题,带电粒子在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,知道半径公式及周期公式,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2007?宝坻区一模)如图所示,在斜面顶端的A点以速度v平抛一小球经t1时间落到斜面上B点处,若在A点将此小球以速度0.5v水平抛出,经t2落到斜面上的C点处,以下判断正确的是( )
(2007?宝坻区一模)如图所示,在斜面顶端的A点以速度v平抛一小球经t1时间落到斜面上B点处,若在A点将此小球以速度0.5v水平抛出,经t2落到斜面上的C点处,以下判断正确的是( )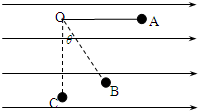 (2007?宝坻区一模)如图所示,在沿水平方向的匀强电场中有一固定点O,用一根长度为l=0.40m的绝缘细线把质量为m=0.20kg,带有正电荷的金属小球悬挂在O点,小球静止在B点时细线与竖直方向的夹角为θ=37°.现将小球拉至位置A使细线水平后由静止释放,求:
(2007?宝坻区一模)如图所示,在沿水平方向的匀强电场中有一固定点O,用一根长度为l=0.40m的绝缘细线把质量为m=0.20kg,带有正电荷的金属小球悬挂在O点,小球静止在B点时细线与竖直方向的夹角为θ=37°.现将小球拉至位置A使细线水平后由静止释放,求: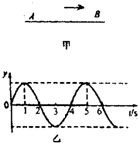 (2007?宝坻区一模)一列简谐横波以1m/s的速度沿绳子由A向B传播,质点A、B间的水平距离x=3m,如图甲所示.若t=0时,质点A正从平衡位置向上振动;其振动图象如图乙所示,则B点的振动图象为下图中的( )
(2007?宝坻区一模)一列简谐横波以1m/s的速度沿绳子由A向B传播,质点A、B间的水平距离x=3m,如图甲所示.若t=0时,质点A正从平衡位置向上振动;其振动图象如图乙所示,则B点的振动图象为下图中的( )