题目内容
 如图所示为某粮仓中由两台皮带传送机组成的传输装置示意图.设备调试时,将倾斜传送机的传送带与水平地面间调成倾角θ=37°,使水平传送机的转动轮边缘以5m/s的线速度沿顺时针方向匀速转动.A、B两端相距L=3m,C、D两端相距较远.现将质量m=10kg的一袋大米无初速的放在A端,它随传送带到大B端后,速度大小不变地传到倾斜传送带的C端,米袋与两传送带之间的动摩擦因数均为μ=0.5,最大静摩擦力大小与滑动摩擦力大小相等(已知g=10m/s2、sin37°=0.6、cos37°=0.8,传送机运动时传送带与转动轮之间无滑动).
如图所示为某粮仓中由两台皮带传送机组成的传输装置示意图.设备调试时,将倾斜传送机的传送带与水平地面间调成倾角θ=37°,使水平传送机的转动轮边缘以5m/s的线速度沿顺时针方向匀速转动.A、B两端相距L=3m,C、D两端相距较远.现将质量m=10kg的一袋大米无初速的放在A端,它随传送带到大B端后,速度大小不变地传到倾斜传送带的C端,米袋与两传送带之间的动摩擦因数均为μ=0.5,最大静摩擦力大小与滑动摩擦力大小相等(已知g=10m/s2、sin37°=0.6、cos37°=0.8,传送机运动时传送带与转动轮之间无滑动).(1)求米袋从A端运动到B端所用的时间;
(2)若倾斜传送带CD不运动,则米袋沿传送带CD所能上滑的最大距离是多少?
(3)将倾斜传送带开动使转动轮沿顺时针方向转动时发现,无论转动速度多大,米袋都无法运送到距C端较远的D端,试分析其原因.欲使米袋能运送到D端应怎样调试倾斜的传送带?
分析:(1)米袋在滑动摩擦力作用下做匀加速直线运动,当速度达到传送带速度时米袋开始匀速直线运动,分两种运动情况分段求解时间即可;
(2)米袋在重力、滑动摩擦力、斜面支持力下沿斜传送带向上匀减速直线运动,根据受力分析求出米袋上滑的合外力,根据牛顿第二定律求出加速度,再根据匀减速直线运动规律求解即可;
(3)当斜传送带顺时针运动时,根据受力特点可以求出米袋上滑的最大距离,要使米袋能达到较远的D点,则须满足米袋受到的摩擦力大于米袋的重力的下滑力.由于动摩擦因数不可改变,所以可以改变传送带倾角可以实现米袋到达D点.
(2)米袋在重力、滑动摩擦力、斜面支持力下沿斜传送带向上匀减速直线运动,根据受力分析求出米袋上滑的合外力,根据牛顿第二定律求出加速度,再根据匀减速直线运动规律求解即可;
(3)当斜传送带顺时针运动时,根据受力特点可以求出米袋上滑的最大距离,要使米袋能达到较远的D点,则须满足米袋受到的摩擦力大于米袋的重力的下滑力.由于动摩擦因数不可改变,所以可以改变传送带倾角可以实现米袋到达D点.
解答:解:(1)米袋在传送带的滑动摩擦力作用下做匀加速直线运动,在水平方向开始只受滑动摩擦力故有:F合=f=μmg=ma1
所以米袋的加速度为:a1=μg=5m/s2
米袋在水平传送带上的最大速度为vmax=5m/s,所以其加速时间为t1=
=1s,这过程中米袋的位移为:x1=
a1
=2.5m
∵x1<L
∴米袋匀速运动位移为:x2=L-x1=0.5m
米袋匀速运动时间为:t2=
=0.1s
所以米袋从A到B的时间为:t=t1+t2=1.1s
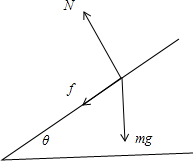 (2)如图米袋在斜传送带上的受力:
(2)如图米袋在斜传送带上的受力:
米袋在斜传送带上所受合力为:
=mgsinθ+f=mgsinθ+μmgcosθ
根据牛顿第二定律米袋产生的加速度为:
a2=
=gsinθ+μgcosθ=10m/s2
因为合力方向沿传送带向下,故米袋做匀减速直线运动,则米袋在CD上上升的最大距离为:
Xmax=
=
m=1.25m
(3)因为mgsinθ>μmgcosθ,所以无论传送带如何顺时针转动,米袋所受合力均沿传送带向下
以米袋向上运动过程中滑摩擦力始终沿传送带向上,此时米袋产生的加速度a3=gsinθ-μgcosθ=2m/s2,所以米袋上升的最大距离为:
x3=
=6.25m
因为CD相距较远,超过了6.25m,所以米袋无法到达D点.
根据题意,调试使米袋可以到达D点,只有减小传送带的倾角θ即可.
答:(1)A至B端所用时间为1.1s;
(2)传送带不动,米袋在CD上上滑的最大距离为1.25m;
(3)调试的方法是减小传送带的倾角θ.
所以米袋的加速度为:a1=μg=5m/s2
米袋在水平传送带上的最大速度为vmax=5m/s,所以其加速时间为t1=
| vmax |
| a1 |
| 1 |
| 2 |
| t | 2 1 |
∵x1<L
∴米袋匀速运动位移为:x2=L-x1=0.5m
米袋匀速运动时间为:t2=
| x2 |
| vmax |
所以米袋从A到B的时间为:t=t1+t2=1.1s
 (2)如图米袋在斜传送带上的受力:
(2)如图米袋在斜传送带上的受力:米袋在斜传送带上所受合力为:
| F | ′ 合 |
根据牛顿第二定律米袋产生的加速度为:
a2=
| ||
| m |
因为合力方向沿传送带向下,故米袋做匀减速直线运动,则米袋在CD上上升的最大距离为:
Xmax=
| ||
| 2a2 |
| 52 |
| 2×10 |
(3)因为mgsinθ>μmgcosθ,所以无论传送带如何顺时针转动,米袋所受合力均沿传送带向下
以米袋向上运动过程中滑摩擦力始终沿传送带向上,此时米袋产生的加速度a3=gsinθ-μgcosθ=2m/s2,所以米袋上升的最大距离为:
x3=
| ||
| 2a3 |
因为CD相距较远,超过了6.25m,所以米袋无法到达D点.
根据题意,调试使米袋可以到达D点,只有减小传送带的倾角θ即可.
答:(1)A至B端所用时间为1.1s;
(2)传送带不动,米袋在CD上上滑的最大距离为1.25m;
(3)调试的方法是减小传送带的倾角θ.
点评:灵活判断摩擦力的存在与否,并由此判断物体的运动性质,根据运动性质分析描述运动的物理量是解决本题的关键

练习册系列答案
相关题目


