题目内容
如图所示，一儿童玩具静止在水平地面上，一个幼儿用与水平面成53°角的恒力拉着它沿水平面运动，已知拉力F=4.0N，玩具的质量m=0.5kg，经过时间t=2.0s，玩具移动了距离x=4.8m，这时幼儿松开手，玩具又滑行了一段距离后停下来．（取g=10m/s2．sin53°=0.8，
cos53°=0.6）
（1）玩具在松手之前的加速度？
（2）全过程玩具的最大速度是多大？
（3）松开手后玩具还能滑行多远？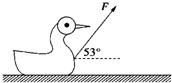
cos53°=0.6）
（1）玩具在松手之前的加速度？
（2）全过程玩具的最大速度是多大？
（3）松开手后玩具还能滑行多远？
（1）由x=
at2，得a=
=2.4m/s2．
（2）松手时，玩具的速度最大，v=at=2.4×2m/s=4.8m/s．
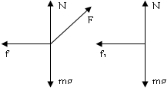
（3）对松手前玩具进行受力分析（如下左图）
Fcos53°-f=ma，
N+Fsin53°=mg
得：f=1.2N，N=1.8N．
所以μ=
=
=
松手后对玩具进行受力分析（如下右图）
a′=
=
=μg=
m/s2
所以还能滑行的距离x′=
=
m=1.728m
| 1 |
| 2 |
| 2x |
| t2 |
（2）松手时，玩具的速度最大，v=at=2.4×2m/s=4.8m/s．
（3）对松手前玩具进行受力分析（如下左图）
Fcos53°-f=ma，
N+Fsin53°=mg
得：f=1.2N，N=1.8N．
所以μ=
| f |
| N |
| 1.2 |
| 1.8 |
| 2 |
| 3 |
松手后对玩具进行受力分析（如下右图）
a′=
| f |
| m |
| μmg |
| m |
| 20 |
| 3 |
所以还能滑行的距离x′=
| 0-v2 |
| -2a′ |
| 4．82 | ||
|
练习册系列答案
53随堂测系列答案
相关题目
如图所示，一儿童玩具静止在水平地面上，一个幼儿用与水平面成53°角的恒力拉着它沿水平面运动，已知拉力F=4.0N，玩具的质量m=0.5kg，经过时间t=2.0s，玩具移动了距离x=4.8m，这时幼儿松开手，玩具又滑行了一段距离后停下来．（取g=10m/s2．sin53°=0.8，
如图所示，一儿童玩具静止在水平地面上，一个幼儿沿与水平面成53°角的恒力拉着它沿水平面运动，已知拉力F=4.0N，玩具的质量m=0.5kg，经过时间t=2.0s，玩具移动了距离x=4.8m，这时幼儿松开手，玩具又滑行了一段距离后停下．
如图所示，一儿童玩具静止在水平地面上，一个幼儿沿与水平面成53°角的恒力拉着它沿水平面运动，已知拉力F=4.0N，玩具的质量m=0.5kg，经过时间t=2.0s，玩具移动了距离x=6m，这时幼儿松开手，玩具又滑行了一段距离后停下．求：