Question

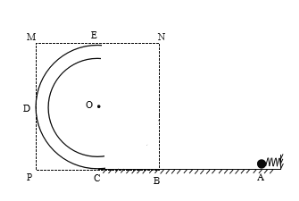
【题目】如图所示，轻质弹簧右端固定，左端与一带电量为+q的小球接触，但不粘连。施加一外力，使它静止在A点，此时弹簧处于压缩状态，小球的质量为m=0.5kg，撤去外力后，小球沿粗糙水平面AC进入竖直的光滑半圆形管道，管道的宽度忽略不计，管道半径r=1m，在边长为2m的正方形BPMN区域内有一匀强电场，电场强度大小为E=，方向与水平方向成45o斜向右上，半圆形轨道外边缘恰好与电场边界相切。水平轨道AB的长度为L=2m，小球与水平面的动摩擦因数μ=0.5，小球到达B点时，速度的大小为m/s，所有的接触面均绝缘，g取10m/s2，求：

(1)释放小球前，弹簧的弹性势能大小；

(2)求小球过D点的速度；

(3)求小球的落地点到C点的距离。

Answer 1

【答案】(1)17.5J(2)m/s(3)(2+1) m

【解析】

(1)对小球从A到B过程，应用动能定理得：

-μmgL+W弹=mvB2-0

W弹=Ep

得：

Ep=17.5J

(2)当小球进入电场后受力分析可得

mg=qEsinθ

故小球在BC粗糙水平面上运动时，对地面的压力为0，不受摩擦力。

F合=qEcosθ=mg

方向水平向右，小球从 B 到 D，应用动能定理可得：

-F合2r=mvD2-mvB2

得：

vD=m/s

(3)从 B 到 N，合外力做功为0

vN=vB=5m/s

由竖直方向运动

2r=gt2

得：

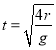
则水平位移大小

x=vNt=2m

则落地点F距离C点的距离为

lCF =(2+1) m