题目内容
如图所示,半径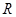 =1.25m的l/4光滑圆弧轨道
=1.25m的l/4光滑圆弧轨道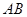 竖直固定,其末端
竖直固定,其末端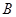 切线水平,并与水平传送带相连,已知小滑块的质量为
切线水平,并与水平传送带相连,已知小滑块的质量为 =0.5kg,滑块与传送带间的动摩擦因数
=0.5kg,滑块与传送带间的动摩擦因数 =0.1,传送带
=0.1,传送带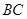 长度为
长度为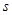 =1.5m,
=1.5m, 、
、 两轮半径
两轮半径 =0.4m,当传送带静止时,用
=0.4m,当传送带静止时,用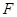 ="4" N的水平拉力将滑块从
="4" N的水平拉力将滑块从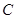 端由静止开始向左拉动。
端由静止开始向左拉动。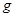 取10m/s2。
取10m/s2。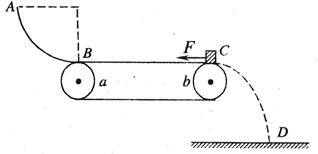
(1)若滑块到达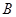 端时撤去拉力
端时撤去拉力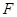 ,求:滑块沿弧形槽上升的最大高度;
,求:滑块沿弧形槽上升的最大高度;
(2)问题(1)中的滑块,从高点沿弧形槽再滑回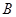 端时,轨道对滑块的支持力多大?
端时,轨道对滑块的支持力多大?
(3)若拉力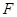 作用一段距离后撤去,滑块到达光滑曲面某一高度而下滑时,以
作用一段距离后撤去,滑块到达光滑曲面某一高度而下滑时,以 、
、 两轮以 角速度
两轮以 角速度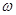 =15rad/s顺时针转动,为使滑块能在
=15rad/s顺时针转动,为使滑块能在 轮最高点
轮最高点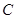 离开传送带飞出,则拉力
离开传送带飞出,则拉力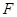 作用的最短距离需多大?
作用的最短距离需多大?
(1)h=1.05m(2)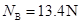 (3)
(3)
解析试题分析:(1)根据动能定理有 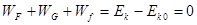
即: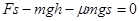 ,代入数值解得h=1.05m
,代入数值解得h=1.05m
(2)从高点滑回B点过程中,根据机械能守恒定律有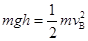
在B点有 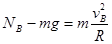 ,
,
解以上两式得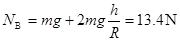
(3)根据题意,滑块要从b轮最高点C离开传送带飞出,则滑块运动至C点的速度最小为  ,即
,即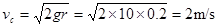
由于传送带的速度v带=rω=6m/s,滑块在B点的速度 ,要使滑块从C点以
,要使滑块从C点以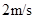 飞出,可分析,滑块在传送带上从B到C做匀加速运动。根据牛顿第二定律,可得加速度
飞出,可分析,滑块在传送带上从B到C做匀加速运动。根据牛顿第二定律,可得加速度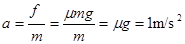
为了使滑块运动到C点时速度大于2m/s,则B点的速度最小为: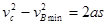 ,代入数据可得
,代入数据可得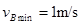
设拉力F作用的最短距离为x,则根据动能定理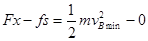
代入数据可以求得
考点:动能定理、机械能守恒定律、圆周运动、牛顿第二定律
点评:利用功能关系解决动力问题是比较基本的解题思路。

 阅读快车系列答案
阅读快车系列答案 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,其圆心角θ=106°,两端点A、B连线水平,质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑.已知平台与AB连线高度差为h=0.8m(已知sin53°=0.8)
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,其圆心角θ=106°,两端点A、B连线水平,质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑.已知平台与AB连线高度差为h=0.8m(已知sin53°=0.8)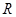 =1.25m的l/4光滑圆弧轨道
=1.25m的l/4光滑圆弧轨道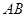 竖直固定,其末端
竖直固定,其末端 切线水平,并与水平传送带相连,已知小滑块的质量为
切线水平,并与水平传送带相连,已知小滑块的质量为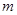 =0.5kg,滑块与传送带间的动摩擦因数
=0.5kg,滑块与传送带间的动摩擦因数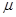 =0.1,传送带
=0.1,传送带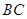 长度为
长度为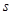 =1.5m,
=1.5m,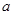 、
、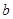 两轮半径
两轮半径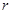 =0.4m,当传送带静止时,用
=0.4m,当传送带静止时,用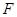 ="4" N的水平拉力将滑块从
="4" N的水平拉力将滑块从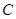 端由静止开始向左拉动。
端由静止开始向左拉动。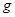 取10m/s2。
取10m/s2。
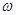 =15rad/s顺时针转动,为使滑块能在
=15rad/s顺时针转动,为使滑块能在 =1.25m的l/4光滑圆弧轨道
=1.25m的l/4光滑圆弧轨道 竖直固定,其末端
竖直固定,其末端 切线水平,并与水平传送带相连,已知小滑块的质量为
切线水平,并与水平传送带相连,已知小滑块的质量为 =0.5kg,滑块与传送带间的动摩擦因数
=0.5kg,滑块与传送带间的动摩擦因数 =0.1,传送带
=0.1,传送带 长度为
长度为 =1.5m,
=1.5m, 、
、 两轮半径
两轮半径 =0.4m,当传送带静止时,用
=0.4m,当传送带静止时,用 ="4"
N的水平拉力将滑块从
="4"
N的水平拉力将滑块从 端由静止开始向左拉动。
端由静止开始向左拉动。 取10m/s2。
取10m/s2。
 =15rad/s顺时针转动,为使滑块能在
=15rad/s顺时针转动,为使滑块能在 =1.25m的l/4光滑圆弧轨道
=1.25m的l/4光滑圆弧轨道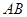 竖直固定,其末端
竖直固定,其末端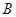 切线水平,并与水平传送带相连,已知小滑块的质量为
切线水平,并与水平传送带相连,已知小滑块的质量为 =0.5kg,滑块与传送带间的动摩擦因数
=0.5kg,滑块与传送带间的动摩擦因数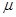 =0.1,传送带
=0.1,传送带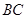 长度为
长度为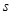 =1.5m,
=1.5m,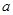 、
、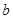 两轮半径
两轮半径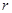 =0.4m,当传送带静止时,用
=0.4m,当传送带静止时,用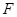 ="4"
N的水平拉力将滑块从
="4"
N的水平拉力将滑块从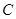 端由静止开始向左拉动。
端由静止开始向左拉动。 取10m/s2。
取10m/s2。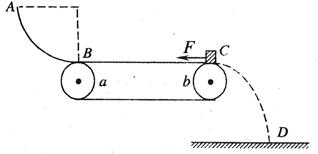
 =15rad/s顺时针转动,为使滑块能在
=15rad/s顺时针转动,为使滑块能在