题目内容
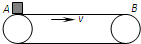如图所示，一水平传送带长为5m，以2m/s的速度做匀速运动．已知某物体与传送带间的动摩擦因数为0.2，现将该物体由静止轻放到传送带的A端．求物体被送到另一端B点所需的时间为（g 取10m/s2）（ ）分析：物体在摩擦力的作用下加速运动，先根据牛顿第二定律求解出加速度，然后假设一直加速，根据运动学公式求出加速的位移，再判断物体有没有到达B端，发现没有到达B端，接下来物体做匀速运动直到B端，分两个匀加速和匀速两个过程，分别求出这两个过程的时间即可．
解答：解：设运动过程中物体的加速度为a，根据牛顿第二定律得
μmg=ma
求得a=2m/s2
设达到皮带速度v时发生的位移为s1，所用时间为t1，则
v2=2as1
解得
s1=1m
根据速度公式有v=at1
解得时间t1=1s
此时距离B端s2=5m-s1=5-1=4m
接下来做匀速运动的时间t2=
=2s
所以t=t1+t2=3s
故选D．
μmg=ma
求得a=2m/s2
设达到皮带速度v时发生的位移为s1，所用时间为t1，则
v2=2as1
解得
s1=1m
根据速度公式有v=at1
解得时间t1=1s
此时距离B端s2=5m-s1=5-1=4m
接下来做匀速运动的时间t2=
| s2 |
| v |
所以t=t1+t2=3s
故选D．
点评：本题关键要对滑块受力分析后，根据牛顿第二定律求解出加速度，再结合运动学公式列式求解．
练习册系列答案
寒假学与练系列答案
相关题目
如图所示．一水平传送装置有轮半径为R=
（2012?聊城模拟）如图所示，一水平传送装置由轮半径均为R=
m的主动轮Q1和从动轮Q2及传送带等构成。两轮轴心相距8m，轮与传送带不打滑，现用此装置运送一袋面粉（可视为质点），已知这袋面粉与传送带之间的动摩擦因数为m＝0.4，这袋面粉中的面粉可不断地从袋中渗出。
m的主动轮
和从动轮
及传送带等构成。两轮轴心相距8.0 m，轮与传送带不打滑。现用此装置运送一袋面粉，已知这袋面粉与传送带之间的动摩擦因素为μ = 0.4，这袋面粉中的面粉可不断地从袋中渗出。（g取10 m/s2）
m的主动轮Q1和从动轮Q2及传送带等构成．两轮轴心相距lAB＝8.0 m，轮与传送带不打滑．现用此装置运送一袋面粉，已知这袋面粉与传送带之间的动摩擦因数μ＝0.4，这袋面粉中的面粉可不断地从袋中渗出．(g取10 m/s2)