题目内容
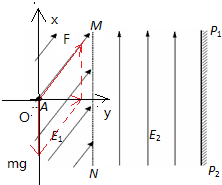
(2012?东至县二模)如图甲所示,在边界MN左侧存在斜方向的匀强电场E1;在MN的右侧有竖直向上、场强大小为E2=0.4N/C的匀强电场,还有垂直纸面向内的匀强磁场B(图甲中未画出)和水平向右的匀强电场E3(图甲中未画出),B和E3随时间变化的情况如图乙所示,P1P2为距MN边界2.28m的竖直墙壁,现有一带正电微粒质量为4×10-7kg,电量为1×10-5C,从左侧电场中距MN边界
m的A处无初速释放后沿直线运动,最后以1m/s的速度垂直MN边界进入右侧场区,设此时刻t=0,取g=10m/s2.求:
(1)MN左侧匀强电场的电场强度E1(sin37°=0.6);
(2)带电微粒在MN右侧场区中运动了1.5s时的速度;
(3)带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?(
≈0.19)

| 1 |
| 2 |
(1)MN左侧匀强电场的电场强度E1(sin37°=0.6);
(2)带电微粒在MN右侧场区中运动了1.5s时的速度;
(3)带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?(
| vB2 |
| R |

分析:该题中(1)是带电粒子在匀强电场和重力场中的运动,对微粒做出正确的受力分析,可以得到正确的结果.在(2)问中,首先要判定微粒的重力和电场力E2q是一对平衡力,然后结合图1,分析在不同的时间段内的受力和运动,即可解答.第三问较为复杂,要先计算出在0s∽1s时间内带电微粒前进距离和带电微粒在磁场B中作圆周运动的半径,判定微粒在第一个周期内是否会打在墙壁上,若不能,再计算出在2.0s∽3s时间内带电微粒前进距离和带电微粒在磁场B中作圆周运动的半径,判定微粒在第二个周期内是否会打在墙壁上,判定的结果是能够打在墙壁上,画出轨迹图象,即可做出正确的判定.
解答:解:(1)设MN左侧匀强电场场强为E1,方向与水平方向夹角为θ.
带电小球受力如右图.
沿水平方向有 qE1cosθ=ma
沿竖直方向有 qE1sinθ=mg
对水平方向的匀加速运动有 v2=2as
代入数据可解得 E1=0.5N/C,θ=53°
即E1大小为0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在MN右侧场区始终满足 qE2=mg
在0∽1s时间内,带电微粒在E3电场中 a=
=
=0.1m/s2
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s
在1∽1.5s时间内,带电微粒在磁场B中运动,
周期为 T=
=
=1s
在1∽1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在MN右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(3)在0s∽1s时间内带电微粒前进距离 s1=vt+
at2=1×1+
×0.1×12=1.05m
带电微粒在磁场B中作圆周运动的半径 r=
=
=
m
因为r+s1<2.28m,所以在1s∽2s时间内带电微粒未碰及墙壁.
在2s∽3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2,
在3s内带电微粒共前进距离
s3=vt3+
at32=1×2+
×0.1×22=2.2m
在3s时带电微粒的速度大小为 v3=v+at3=1+0.1×2=1.2m/s
在3s∽4s时间内带电微粒在磁场B中作圆周运动的半径r3=
=
=
m=0.19m
因为r3+s3>2.28m,所以在4s时间内带电微粒碰及墙壁.
带电微粒在3s以后运动情况如右图,

其中 d=2.28-2.2=0.08m
sinθ=
=0.5,θ=30°
所以,带电微粒作圆周运动的时间为t3=
=
=
=
s
带电微粒与墙壁碰撞的时间为 t总=3+
=
s
答:(1)MN左侧匀强电场的电场强度E1=0.5N/C,方向与水平向右方向夹53°角斜向上;(2)带电微粒在MN右侧场区中运动了1.5s时的速度为1.1m/s,方向水平向左;
(3)带电微粒在MN右侧场区中与墙壁碰撞前运动的时间为
s.
带电小球受力如右图.

沿水平方向有 qE1cosθ=ma
沿竖直方向有 qE1sinθ=mg
对水平方向的匀加速运动有 v2=2as
代入数据可解得 E1=0.5N/C,θ=53°
即E1大小为0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在MN右侧场区始终满足 qE2=mg
在0∽1s时间内,带电微粒在E3电场中 a=
| qE3 |
| m |
| 1×10-5×0.004 |
| 4×10-7 |
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s
在1∽1.5s时间内,带电微粒在磁场B中运动,
周期为 T=
| 2πm |
| qB |
| 2π×4×10-7 |
| 1×10-5×0.08π |
在1∽1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在MN右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(3)在0s∽1s时间内带电微粒前进距离 s1=vt+
| 1 |
| 2 |
| 1 |
| 2 |
带电微粒在磁场B中作圆周运动的半径 r=
| mv |
| qB |
| 4×10-7×1.1 |
| 1×10-5×0.08π |
| 1.1 |
| 2π |
因为r+s1<2.28m,所以在1s∽2s时间内带电微粒未碰及墙壁.
在2s∽3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2,
在3s内带电微粒共前进距离
s3=vt3+
| 1 |
| 2 |
| 1 |
| 2 |
在3s时带电微粒的速度大小为 v3=v+at3=1+0.1×2=1.2m/s
在3s∽4s时间内带电微粒在磁场B中作圆周运动的半径r3=
| mv3 |
| qB |
| 4×10-7×1.2 |
| 1×10-5×0.08π |
| 1.2 |
| 2π |
因为r3+s3>2.28m,所以在4s时间内带电微粒碰及墙壁.
带电微粒在3s以后运动情况如右图,

其中 d=2.28-2.2=0.08m
sinθ=
| d |
| r3 |
所以,带电微粒作圆周运动的时间为t3=
| T3 |
| 12 |
| 2πm |
| 12qB |
| 2π×4×10-7 |
| 12×1×10-5×0.08π |
| 1 |
| 12 |
带电微粒与墙壁碰撞的时间为 t总=3+
| 1 |
| 12 |
| 37 |
| 12 |
答:(1)MN左侧匀强电场的电场强度E1=0.5N/C,方向与水平向右方向夹53°角斜向上;(2)带电微粒在MN右侧场区中运动了1.5s时的速度为1.1m/s,方向水平向左;
(3)带电微粒在MN右侧场区中与墙壁碰撞前运动的时间为
| 37 |
| 12 |
点评:该题考查带电微粒在电场和磁场中的运动,情景复杂,头绪较多,解答的过程中,要对各种情景有非常清晰的判断,才能理清头绪,正确作答.题目难度大.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2012?东至县二模)如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数?=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2)
(2012?东至县二模)如图,半径R=1.0m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=0.5m的水平面BC相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=37°的光滑斜面连接,质量m=1.0kg的小滑块从圆弧上某点由静止释放,到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰,碰后返回恰好停在B点,已知滑块与水平面间的动摩擦因数?=0.1.(sin37°=0.6 cos37°=0.8,g取l0m/s2) (2012?东至县二模)如图所示,质量为10kg的物体A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为5N时,物体A处于静止状态.若小车以1m/s2的加速度向右运动后,则(g=10m/s2)( )
(2012?东至县二模)如图所示,质量为10kg的物体A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为5N时,物体A处于静止状态.若小车以1m/s2的加速度向右运动后,则(g=10m/s2)( )