题目内容
2. 质量为M,倾角为30°的光滑斜面静止在粗糙的水平地面上,斜面上两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧相连,现对小球B施加一水平向左的拉力F,使A、B及斜面一起向左做匀速直线运动,如图所示.已知弹簧的原长为l0,求:
质量为M,倾角为30°的光滑斜面静止在粗糙的水平地面上,斜面上两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧相连,现对小球B施加一水平向左的拉力F,使A、B及斜面一起向左做匀速直线运动,如图所示.已知弹簧的原长为l0,求:(1)此时弹簧的长度l;
(2)水平拉力F的大小;
(3)粗糙地面与斜面体间的动摩擦因数μ.
分析 (1)以球A为研究对象,受力分析后根据平衡条件列式求解弹簧弹力,然后结合胡克定律列式求解弹簧的伸长量和长度;
(2)以A、B及弹簧整体为研究对象,受力分析后根据平衡条件列式求解;
(3)以A、B、斜面及弹簧整体为研究对象,受力分析后根据共点力平衡条件列式求解摩擦力和支持力,最后根据滑动摩擦定律列式求解动摩擦因素.
解答 解:(1)以A为研究对象,受重力、拉力和支持力,根据平衡条件,有:k(l-l0)=mgsin30°
解得:l=$\frac{mg}{2k}$+l0
(2)以A、B及弹簧整体为研究对象,受拉力、滑动摩擦力、重力和支持力,根据平衡条件,有:Fcos30°=2mgsin30°
解得:F=$\frac{2}{3}\sqrt{3}$mg
(3)以A、B、斜面及弹簧整体为研究对象,根据平衡条件,有:F=f=μ(M+2m)g
解得:μ=$\frac{2\sqrt{3}m}{3(M+2m)}$
答:
(1)此时弹簧的长度l为$\frac{mg}{2k}$+l0;
(2)水平拉力F的大小为$\frac{2}{3}\sqrt{3}$mg;
(3)粗糙地面与斜面体间的动摩擦因素μ为$\frac{2\sqrt{3}m}{3(M+2m)}$.
点评 对于连接体问题注意整体与隔离法的应用,正确选取研究对象然后受力分析,根据所处状态列方程求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.一铁块沿斜面释放后滑下,恰好作匀速运动,那么在下滑过程中( )
| A. | 铁块机械能减小量等于铁块内能增加量 | |
| B. | 铁块机械能守恒,内能不变 | |
| C. | 铁块具有的总能量减少 | |
| D. | 铁块具有的总能量增加 |
19.下列关于匀速圆周运动的说法中,正确的是( )
| A. | 向心加速度是描述角速度变化的快慢的 | |
| B. | 向心加速度是描述线速度大小变化的快慢的 | |
| C. | 向心加速度恒定不变 | |
| D. | 向心加速度是描述线速度方向变化的快慢的 |
 如图所示,将小螺线管A插入大螺线管B中不动.(1)~(3)问(填“有”或“无”).
如图所示,将小螺线管A插入大螺线管B中不动.(1)~(3)问(填“有”或“无”).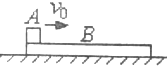 如图所示,一小铁块A以某一水平速度冲上放置在光滑水平面上的木板B上,由于A、B之间的摩擦力作用,小铁块A相对于木板B滑行了一段距离d,两者就相对静止,已知A、B之间的滑动摩擦力为Fμ,试求这一过程中系统中产生的热量.
如图所示,一小铁块A以某一水平速度冲上放置在光滑水平面上的木板B上,由于A、B之间的摩擦力作用,小铁块A相对于木板B滑行了一段距离d,两者就相对静止,已知A、B之间的滑动摩擦力为Fμ,试求这一过程中系统中产生的热量.