题目内容
2. 如图所示,置于水平面上两根平行导轨间距离为d=0.5m,金属细杆ab置于导轨一端;跨在两导轨之间,它与每根导轨之间的最大静摩擦力为fmax=0.2N,导轨另一端用直导线相连,形成一个恰是矩形的回路.导轨长l=0.8m,电路中只有ab有电阻,R=0.2Ω,整个装置置于磁场方向竖直向下的匀强磁场中,如果磁感应强度从B0=1T瞬间开始,以0.2T/s的变化率均匀地增大,求:
如图所示,置于水平面上两根平行导轨间距离为d=0.5m,金属细杆ab置于导轨一端;跨在两导轨之间,它与每根导轨之间的最大静摩擦力为fmax=0.2N,导轨另一端用直导线相连,形成一个恰是矩形的回路.导轨长l=0.8m,电路中只有ab有电阻,R=0.2Ω,整个装置置于磁场方向竖直向下的匀强磁场中,如果磁感应强度从B0=1T瞬间开始,以0.2T/s的变化率均匀地增大,求:(1)经过多长时间后,ab杆开始运动?
(2)杆运动前回路中产生的热量是多少?
(3)杆运动前,通过ab杆横截面的电荷量是多少?
分析 (1)磁感应强度均匀增大时,穿过回路的磁通量均匀增大,回路中产生恒定的感应电动势和感应电流,ab受到的安培力均匀增大,当它所受的安培力等于大静摩擦力fmax时将开始运动,由平衡条件求出此时的感应电流,由法拉第电磁感应定律和欧姆定律结合求出此时的磁感应强度B,结合B的变化率就能求出时间.
(2)根据焦耳定律求解热量;
(3)根据电量的综合表达式$q=N\frac{△∅}{R}$,即可求解.
解答 解:(1)设回路中产生的感应电动势大小为E,感应电流大小为I,由法拉第电磁感应定律得:
E=$\frac{△∅}{△t}$=$\frac{△B}{△t}$ld=0.2×0.8×0.5V=0.08V
根据闭合电路欧姆定律得:
I=$\frac{E}{R}$=$\frac{0.08}{0.2}$A=0.4A
当ab棒刚开始运动时,它所受的安培力等于大静摩擦力fmax,设此时的磁感应强度为B,则有:
BId=fmax,
得:B=$\frac{{f}_{max}}{Id}$=$\frac{0.4}{0.4×0.5}$T=2T
所以从加上磁场到ab开始运动所经历的时间为:t=$\frac{B-{B}_{0}}{\frac{△B}{△t}}$=$\frac{2-1}{0.2}$s=5s
(2)杆运动前回路中产生的热量是:Q=I2Rt=0.42×0.2×5J=0.16J
(3)根据电量的综合表达式,$q=N\frac{△∅}{R}$=$\frac{0.2×5}{0.2}$=5C,
答:(1)经过5s时间后,ab杆开始运动.
(2)杆运动前回路中产生的热量是0.16J;
(3)杆运动前,通过ab杆横截面的电荷量是5C.
点评 对于本题要知道磁通量均匀变化时产生的感应电动势和感应电流是一定的,掌握物体刚要运动时静摩擦力达到最大值,并能熟练运用法拉第电磁感应定律和欧姆定律、安培力公式进行处理,同时掌握电量的综合表达式的推导.

 口算题天天练系列答案
口算题天天练系列答案| A. | $\frac{3H}{4}$ | B. | $\frac{H}{2}$ | C. | $\frac{H}{3}$ | D. | $\frac{H}{4}$ |
| A. | 物体的初速度是5m/s | B. | 物体的加速度大小是5m/s2 | ||
| C. | 物体的初速度是10m/s | D. | 物体的加速度大小是2.5m/s2 |
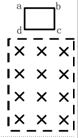 如图所示,闭合矩形线圈abcd从静止开始竖直下落,穿过一个匀强磁场区域,磁场长度远大于线圈长度,不计空气阻力,则此线圈从cd边进入磁场到ab边穿出磁场为止,以下说法中正确的是( )
如图所示,闭合矩形线圈abcd从静止开始竖直下落,穿过一个匀强磁场区域,磁场长度远大于线圈长度,不计空气阻力,则此线圈从cd边进入磁场到ab边穿出磁场为止,以下说法中正确的是( )| A. | 始终有一向下的速度 | B. | 一定有一向下的加速度 | ||
| C. | 加速度可能为零 | D. | 加速度可能向上 |
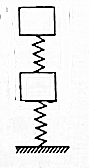
| A. | 弹簧k1在上,物块M在上 | B. | 弹簧k1在上,物块m在上 | ||
| C. | 弹簧k2在上,物块M在上 | D. | 弹簧k2在上,物块m在上 |
 如图是我国过去农村人拉耧种麦的照片,假设无论怎样变化,耧插入地面的深度不变(即耧所受地面阻力不变),每个人的拉力大小不变,四人始终在耧前与运动方向垂直的一直线上,且人肩上绳距地面的高度不变,那么要增大拉力沿水平方向的合力,可采取的措施是( )
如图是我国过去农村人拉耧种麦的照片,假设无论怎样变化,耧插入地面的深度不变(即耧所受地面阻力不变),每个人的拉力大小不变,四人始终在耧前与运动方向垂直的一直线上,且人肩上绳距地面的高度不变,那么要增大拉力沿水平方向的合力,可采取的措施是( )| A. | 仅增大四个人之间的间距 | B. | 仅减小四个人的间距 | ||
| C. | 仅缩短拉绳 | D. | 仅增长拉绳 |

| A. | 14.14 V 0.0l s | B. | l0 V 0.0l s | ||
| C. | 14.14 V 0.02 s | D. | l0 V 0.02 s |
