题目内容
一个“ ”形导轨PONQ,其质量为M="2.0" kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m="0.60" kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80 T,如图所示。已知导轨ON段长为0.50 m,电阻是0.40 Ω,金属棒CD的电阻是0.20 Ω,其余电阻不计.导轨在水平拉力作用下由静止开始以0.20 m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0 A时,导轨改做匀速直线运动.设导轨足够长,取g=10 m/s2。求:
”形导轨PONQ,其质量为M="2.0" kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m="0.60" kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80 T,如图所示。已知导轨ON段长为0.50 m,电阻是0.40 Ω,金属棒CD的电阻是0.20 Ω,其余电阻不计.导轨在水平拉力作用下由静止开始以0.20 m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0 A时,导轨改做匀速直线运动.设导轨足够长,取g=10 m/s2。求:
⑴导轨运动起来后,C、D两点哪点电势较高?
⑵导轨做匀速运动时,水平拉力F的大小是多少?
⑶导轨做匀加速运动的过程中,水平拉力F的最小值是多少?
⑷CD上消耗的电功率为P="0.80" W时,水平拉力F做功的功率是多大?
(1)C(2)2.48 N (3)1.6 N(4)6.72 W
解析试题分析:(1)根据右手定则,可知C点电势较高。
(2)导轨匀速运动时,CD棒所受安培力:F1="BIL=1.6" N,方向向右
导轨所受摩擦力为: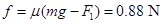 ,方向向右
,方向向右
导轨受安培力:F2="1.6" N,方向向右
水平拉力:F=F2+f="2.48" N。
(3)导轨以加速度a做匀加速运动,速度为v时,有: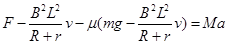 ①
①
当速度为零时,水平力F最小,Fm="1.6" N。
(4)CD上消耗电功率为0.8 W时,电路中的电流为: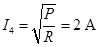
此时由: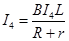
解得导轨运动的速度:v4="3" m/s。
根据①可知:F4="2.24" N
力F做功的功率为P4=F4v4="6.72" W。
考点:本题考查电磁感应综合问题,涉及到匀变速直线运动,牛顿第二定律和电学的相关知识。

质量为m的汽车以恒定的功率P在平直的公路上行驶,汽车匀速行驶时的速率为v1,则当汽车的速率为v2(v2< v1)时,汽车的加速度为( )
| A.P/mv1 | B.P/mv2 | C.2P/m(v1+v2) | D.P(v1-v2)/mv1v2 |
 )的A点静止释放。
)的A点静止释放。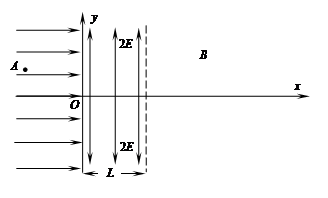


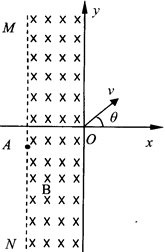
 中,M点的横坐标
中,M点的横坐标 区域内,有竖直向下的匀强电场;N点的横坐标
区域内,有竖直向下的匀强电场;N点的横坐标 以N为圆心、r为半径的圆内及圆边界上有垂直于纸面向里的匀强磁场.P为磁场边界上一点.NP与竖直方向的夹角
以N为圆心、r为半径的圆内及圆边界上有垂直于纸面向里的匀强磁场.P为磁场边界上一点.NP与竖直方向的夹角 .从M点沿
.从M点沿 轴正方向发射一质量为m、电荷量为q的带负电粒子,粒子速度大小为
轴正方向发射一质量为m、电荷量为q的带负电粒子,粒子速度大小为 ,粒子沿过P点的切线方向射出电场。后经P点进人磁场运动且经过N点,不计粒子重力,
,粒子沿过P点的切线方向射出电场。后经P点进人磁场运动且经过N点,不计粒子重力, 求:
求:
 倍。将珠子从环最低位置A点静止释放,求:
倍。将珠子从环最低位置A点静止释放,求:
 倍。粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求:
倍。粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求: