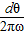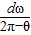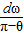题目内容
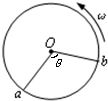
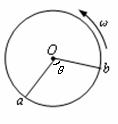
 如图所示,纸质圆筒以角速度ω绕竖直轴O高速转动,一颗子弹沿圆筒截面直径方向穿过圆筒,若子弹在圆筒转动不到半周的过程中在圆筒上留下了两个弹孔a、b.已知Oa和Ob间的夹角为θ<180°,圆筒截面直径为d,则子弹的速度大小为( )
如图所示,纸质圆筒以角速度ω绕竖直轴O高速转动,一颗子弹沿圆筒截面直径方向穿过圆筒,若子弹在圆筒转动不到半周的过程中在圆筒上留下了两个弹孔a、b.已知Oa和Ob间的夹角为θ<180°,圆筒截面直径为d,则子弹的速度大小为( )分析:本题找出在子弹穿过圆筒的时间内,圆筒转过的角度是解决本题的关键,题中提到是在圆筒转动不到半周的过程中穿过的,故转过的角度是π-θ.
解答:解:设子弹的速度为v0,
由题意知,子弹穿过两个孔所需时间t=
…①
纸质圆筒在这段时间内转过角度为π-θ,由角速度的公式有ω=
…②
由①②两式解得v0=
.
故答案为D.
由题意知,子弹穿过两个孔所需时间t=
| d |
| v0 |
纸质圆筒在这段时间内转过角度为π-θ,由角速度的公式有ω=
| π-θ |
| t |
由①②两式解得v0=
| dω |
| π-θ |
故答案为D.
点评:若把原题中的“若子弹在圆筒转动不到半周的过程中”去掉,子弹的速度又如何?

练习册系列答案
相关题目