题目内容
3. 如图所示,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B置于光滑绝缘的水平面上,A球的带电量为+2q,B球的带电量为-3q,构成一个带电系统(它们均可视为质点,也不考虑两者间相互作用的库仑力).现让小球A处在有界匀强电场区域MPNQ内.已知虚线MP位于细杆的中垂线上,虚线NQ与MP平行且间距足够长.匀强电场的电场强度大小为E,方向水平向右.释放带电系统,让它从静止开始运动.
如图所示,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B置于光滑绝缘的水平面上,A球的带电量为+2q,B球的带电量为-3q,构成一个带电系统(它们均可视为质点,也不考虑两者间相互作用的库仑力).现让小球A处在有界匀强电场区域MPNQ内.已知虚线MP位于细杆的中垂线上,虚线NQ与MP平行且间距足够长.匀强电场的电场强度大小为E,方向水平向右.释放带电系统,让它从静止开始运动.求:(1)B球刚进入电场时,带电系统的速度大小?
(2)带电系统运动过程中,B球电势能增加的最大值多少?
分析 (1)对A、B系统,运用动能定理求B球刚进入电场时带电系统的速度.
(2)当带电系统的动能为零,系统的动能全部转化为电势能,对整个过程,运用动能定理求出克服电场力做功的最大值,从而得到B球电势能增加的最大值.
解答 解:(1)设带电系统开始运动时,系统的速度为v1
对A、B系统应用动能定理:2qEL=$\frac{1}{2}$(2m)v12
则v1=$\sqrt{\frac{2qEL}{m}}$
(2)设球A向右运动s时,系统速度为零
由动能定理知:A球电场力做功等于B球克服电场力做功
则 2qE′s=3qE′(s-L)
则s=3L
B球进入电场距离为2L,B球克服电场力做功 WFB=6qEL
则B球电势能增加了6qEL
答:
(1)B球刚进入电场时,带电系统的速度大小是$\sqrt{\frac{2qEL}{m}}$.
(2)带电系统运动过程中,B球电势能增加的最大值是6qEL.
点评 解决本题的关键理清带电系统在整个过程中的运动情况,灵活选择研究过程,运用动能定理求解.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
14.下列物理量中,属于矢量的是( )
| A. | 密度 | B. | 位移 | C. | 时间 | D. | 路程 |
11.下列说法中正确的是( )
| A. | 物体的加速度为零,速度一定为零 | |
| B. | 物体的速度大小保持不变时,加速度一定为零 | |
| C. | 速度变化越快,加速度一定越大 | |
| D. | 加速度小,速度不一定小 |
18.如图是一物体在一条水平直线上运动的v-t图象,以向右为正方向,则( )
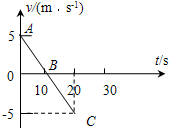
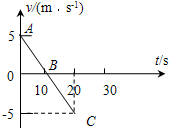
| A. | AB段表示物体向左运动 | B. | AB段表示物体向右运动,速度减小 | ||
| C. | BC段表示物体速度减小 | D. | 全程的加速度是-0.5m/s2 |
8.下列哪些现象是为了防止物体产生离心运动( )
①汽车转弯时要限制车速;
②转动的砂轮半径不能做得很大;
③在修筑铁路时,转弯处轨道的内轨要低于外轨;
④离心水泵工作时.
①汽车转弯时要限制车速;
②转动的砂轮半径不能做得很大;
③在修筑铁路时,转弯处轨道的内轨要低于外轨;
④离心水泵工作时.
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
15.一个氢原子中的电子从一半径为ra的轨道自发地直接跃迁至另一半径为rb的轨道,已知ra>rb,则在此过程中( )
| A. | 原子发出一系列频率的光子 | B. | 原子要吸收一系列频率的光子 | ||
| C. | 原子要吸收某一频率的光子 | D. | 原子要辐射某一频率的光子 |
13. 如图所示,质量为m的物体在一个与水平方向成θ角的拉力F作用下,一直沿水平面向右匀速运动,则下列关于物体在t时间内所受力的冲量的说法中正确的是( )
如图所示,质量为m的物体在一个与水平方向成θ角的拉力F作用下,一直沿水平面向右匀速运动,则下列关于物体在t时间内所受力的冲量的说法中正确的是( )
 如图所示,质量为m的物体在一个与水平方向成θ角的拉力F作用下,一直沿水平面向右匀速运动,则下列关于物体在t时间内所受力的冲量的说法中正确的是( )
如图所示,质量为m的物体在一个与水平方向成θ角的拉力F作用下,一直沿水平面向右匀速运动,则下列关于物体在t时间内所受力的冲量的说法中正确的是( )| A. | 拉力F的冲量大小为Ftcosθ | B. | 摩擦力的冲量大小为Ftcosθ | ||
| C. | 重力的冲量大小为mgt | D. | 物体所受支持力的冲量为零 |
 为了测量干电池的电动势,某同学设计了如图所示的电路.其中:E是待测电池,内阻不能忽略;Vl、V2是两只量程都合适的电压表,内阻不是很大,且未知;Sl、S2是单刀单掷开关;导线若干.
为了测量干电池的电动势,某同学设计了如图所示的电路.其中:E是待测电池,内阻不能忽略;Vl、V2是两只量程都合适的电压表,内阻不是很大,且未知;Sl、S2是单刀单掷开关;导线若干.