题目内容
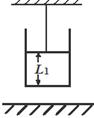
如图7-17所示,一根一端封闭的玻璃管,当L=0.96m,内有一段长h1=0.20m的水银柱。当温度为t1=27℃,开口端竖直向上时,封闭空气柱h2= 0.60m。问温度至少升到多高时,水银柱才能从管中全部溢出?(外界大气压相当于L0= 0.76m高的水银柱产生的压强)

T2=385.2K
【错解分析】错解:以封闭气体为研究对象,其初态:p1=(L0+h1),V1=h2S下;末态是水银刚好完全溢出时的状态:p2=L0,V2=LS
T2=?

上述解答中有一个错误,就是存在“潜在假设”。即认为:水银柱在外溢过程中,气体体积越大,对应温度越高,当气体充满整个玻璃管(即水银全部溢出)时,所对应的温度是最高的。事实是:
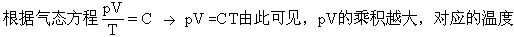 越高。在水银末溢出前,p不变,V越大,T越大。在水银溢出的过程中,p减小,V增大,p·V的乘积并非一直增大。所以我们在解题的过程中,应找出在什么条件下,pV的乘积最大,由此确定相应的温度。
越高。在水银末溢出前,p不变,V越大,T越大。在水银溢出的过程中,p减小,V增大,p·V的乘积并非一直增大。所以我们在解题的过程中,应找出在什么条件下,pV的乘积最大,由此确定相应的温度。
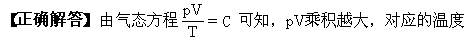 T越高,假设管中还有长为X的水银柱尚未溢出时,pV值最大,即(L0+x)(L-x)S的值最大,这是一个数学求极值问题。因为(L0+x)+(L-x)=(L0+L)与x的大小无关,所以由数学知识可知:两数之和为一常数,则当这两数相等时,其乘积最大。
T越高,假设管中还有长为X的水银柱尚未溢出时,pV值最大,即(L0+x)(L-x)S的值最大,这是一个数学求极值问题。因为(L0+x)+(L-x)=(L0+L)与x的大小无关,所以由数学知识可知:两数之和为一常数,则当这两数相等时,其乘积最大。
所以:L0+x =L-x
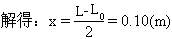
即管内水银柱由0.20m溢出到还剩下0.10m的过程中,p·V的乘积越来越大,这一过程必须是升温的。此后,温度不必再升高(但要继续给气体加热),水银柱也将继续外溢,直至完全溢出。由气态方程:
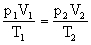

代入数据得:T2=385.2K。
T2=?

上述解答中有一个错误,就是存在“潜在假设”。即认为:水银柱在外溢过程中,气体体积越大,对应温度越高,当气体充满整个玻璃管(即水银全部溢出)时,所对应的温度是最高的。事实是:
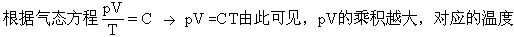 越高。在水银末溢出前,p不变,V越大,T越大。在水银溢出的过程中,p减小,V增大,p·V的乘积并非一直增大。所以我们在解题的过程中,应找出在什么条件下,pV的乘积最大,由此确定相应的温度。
越高。在水银末溢出前,p不变,V越大,T越大。在水银溢出的过程中,p减小,V增大,p·V的乘积并非一直增大。所以我们在解题的过程中,应找出在什么条件下,pV的乘积最大,由此确定相应的温度。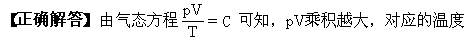 T越高,假设管中还有长为X的水银柱尚未溢出时,pV值最大,即(L0+x)(L-x)S的值最大,这是一个数学求极值问题。因为(L0+x)+(L-x)=(L0+L)与x的大小无关,所以由数学知识可知:两数之和为一常数,则当这两数相等时,其乘积最大。
T越高,假设管中还有长为X的水银柱尚未溢出时,pV值最大,即(L0+x)(L-x)S的值最大,这是一个数学求极值问题。因为(L0+x)+(L-x)=(L0+L)与x的大小无关,所以由数学知识可知:两数之和为一常数,则当这两数相等时,其乘积最大。所以:L0+x =L-x
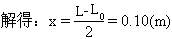
即管内水银柱由0.20m溢出到还剩下0.10m的过程中,p·V的乘积越来越大,这一过程必须是升温的。此后,温度不必再升高(但要继续给气体加热),水银柱也将继续外溢,直至完全溢出。由气态方程:
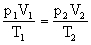

代入数据得:T2=385.2K。

练习册系列答案
相关题目
 两个温度下研究其等温变化的规律,在图所示的p-V图上画出两条双曲线,分别作垂直于纵轴与横轴的直线,交两曲线的点分别为a、b和c、d,与横轴交点为e,已知
两个温度下研究其等温变化的规律,在图所示的p-V图上画出两条双曲线,分别作垂直于纵轴与横轴的直线,交两曲线的点分别为a、b和c、d,与横轴交点为e,已知 =1∶2,则
=1∶2,则
 =1∶3
=1∶3 =1∶3
=1∶3 =1∶3
=1∶3





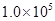 Pa。将右侧气体加热,而左侧仍保持原来温度,平衡时测得左侧气体的压强为p=
Pa。将右侧气体加热,而左侧仍保持原来温度,平衡时测得左侧气体的压强为p=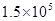 Pa,求:
Pa,求: