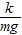题目内容
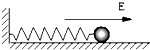 如图所示,一个劲度系数为k由绝缘材料制成的轻弹簧,一端固定,另一端与质量为m的带电量为+q的小球相连,静止在光滑水平面上.当加入如图所示的匀强电场E后,小球开始运动.下列说法正确的是( )
如图所示,一个劲度系数为k由绝缘材料制成的轻弹簧,一端固定,另一端与质量为m的带电量为+q的小球相连,静止在光滑水平面上.当加入如图所示的匀强电场E后,小球开始运动.下列说法正确的是( )分析:小球受到电场力向右运动,当运动到平衡位置时,电场力与弹簧的弹力大小相等,由胡克定律分析可知,弹簧伸长了
,此时小球速度的最大.图示位置小球处于位移最大处,弹簧处于原长,平衡位置时弹簧伸长了
,根据振幅是振动物体离开平衡位置最大的距离,确定振幅的大小.根据简谐运动的对称性,分析弹簧最大的伸长量,由EP=
kx2确定弹簧的最大弹性势能.小球运动过程中小球的电势能、动能和弹簧的弹性势能相互转化,根据能量守恒定律分析总量变化情况.
| qE |
| k |
| qE |
| k |
| 1 |
| 2 |
解答:解:A、小球处于平衡位置时,电场力与弹簧的弹力平衡,弹簧伸长了
,此时小球的速度不是零,而是最大.故A错误.
B、图示位置小球处于位移最大处,弹簧处于原长,平衡位置时弹簧伸长了
,则振幅A=
.故B正确.
C、根据对称性可知,弹簧最大的伸长量x=2A=
,弹簧的最大弹性势能EP=
kx2=
.故C正确.
D、由题,水平面是光滑的,在运动过程中,小球的电势能、动能和弹簧的弹性势能互相转化,根据能量守恒定律可知,三者总量保持不变.故D错误.
故选BC
| qE |
| k |
B、图示位置小球处于位移最大处,弹簧处于原长,平衡位置时弹簧伸长了
| qE |
| k |
| qE |
| k |
C、根据对称性可知,弹簧最大的伸长量x=2A=
| 2qE |
| k |
| 1 |
| 2 |
| 2q2E2 |
| k |
D、由题,水平面是光滑的,在运动过程中,小球的电势能、动能和弹簧的弹性势能互相转化,根据能量守恒定律可知,三者总量保持不变.故D错误.
故选BC
点评:求解振幅关键找到最大位移处与平衡位置之间的距离来确定.简谐运动常常利用对称性和周期性分析物理量的变化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013?丰台区模拟)如图所示,天花板上悬挂着一个劲度系数为k的轻弹簧,弹簧下端系一质量为m的物块.物块处于静止状态时,弹簧的伸长量为(重力加速度为g)( )
(2013?丰台区模拟)如图所示,天花板上悬挂着一个劲度系数为k的轻弹簧,弹簧下端系一质量为m的物块.物块处于静止状态时,弹簧的伸长量为(重力加速度为g)( )