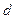题目内容
如下图所示，让摆球从图中的C位置由静止开始摆下，摆到最低点D处，摆线刚好被拉断，小球在粗糙的水平面上由D点向左做匀减速运动，到达小A孔进入半径R=0.3m的竖直放置的光滑圆弧轨道，当摆球进入圆轨道立即关闭A孔。已知摆线长L=2m，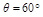
，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2。试求：
小题1:求摆线能承受的最大拉力为多大？
小题2:要使摆球能进入圆轨道并且不脱离轨道，求粗糙水平面摩擦因数μ的范围。
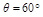，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2。试求：小题1:求摆线能承受的最大拉力为多大？
小题2:要使摆球能进入圆轨道并且不脱离轨道，求粗糙水平面摩擦因数μ的范围。
小题1:10N
小题2:0.35≤μ≤0.5或者μ≤0.125
（1）当摆球由C到D运动机械能守恒：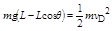
（2分）
由牛顿第二定律可得：
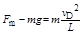（1分）
可得：Fm="2mg=10N" （1分）
（2）小球不脱圆轨道分两种情况：①要保证小球能达到A孔，设小球到达A孔的速度恰好为零，
由动能定理可得：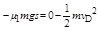
（1分）
可得：μ1="0.5" （1分）
若进入A孔的速度较小，那么将会在圆心以下做等幅摆动，不脱离轨道。其临界情况为到达圆心等高处速度为零，由机械能守恒可得：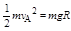
（1分）
由动能定理可得：
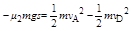（2分）
可求得：μ2=0.35（1分）
②若小球能过圆轨道的最高点则不会脱离轨道，在圆周的最高点由牛顿第二定律可得：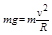
（1分）
由动能定理可得：
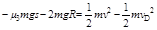（2分）
解得：μ3="0.125" （1分）
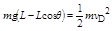（2分）由牛顿第二定律可得：
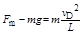（1分）可得：Fm="2mg=10N" （1分）
（2）小球不脱圆轨道分两种情况：①要保证小球能达到A孔，设小球到达A孔的速度恰好为零，
由动能定理可得：
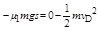（1分） 可得：μ1="0.5" （1分）
若进入A孔的速度较小，那么将会在圆心以下做等幅摆动，不脱离轨道。其临界情况为到达圆心等高处速度为零，由机械能守恒可得：
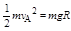（1分）由动能定理可得：
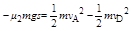（2分）可求得：μ2=0.35（1分）
②若小球能过圆轨道的最高点则不会脱离轨道，在圆周的最高点由牛顿第二定律可得：
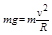（1分）由动能定理可得：
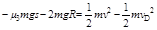（2分）解得：μ3="0.125" （1分）
练习册系列答案
相关题目
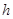高处由静止开始滑下，与滑块B发生碰撞（时间极短）并粘在一起压缩弹簧推动滑块C向前运动，经过一段时间，滑块C脱离弹簧，继续在水平面上做匀速运动。已知
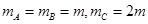,求：
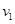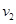大小；
的大小；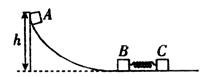
；两个物体均可视为质点，不计绳子和滑轮的质量、不计滑轮轴上的摩擦力和空气阻力。问：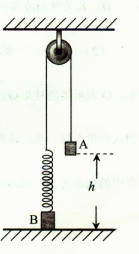
物块Q轻轻地放在弹簧上，当弹簧也被压缩l时，物块Q的加速度和速度的大小分别是多少？
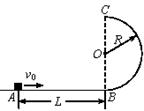
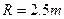的竖直半圆轨道组成，现由水平地面上的A点斜向上抛出一个小球，使之由半圆轨道的最高点B水平进入轨道，沿轨道运动，已知小球冲上弧形轨道的最大高度为
，
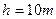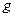取
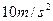。求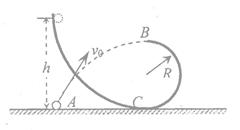
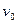的大小和方向