题目内容
某同学利用如图所示的装置测量当地的重力加速度。实验步骤如下:
A.按装置图安装好实验装置; B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度 ; D.让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时,并计数为1,此后小球每经过最低点一次,依次计数2、3……。当数到 n时,停止计时,测得时间为t;
; D.让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时,并计数为1,此后小球每经过最低点一次,依次计数2、3……。当数到 n时,停止计时,测得时间为t;
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;G.以t2为纵坐标、 为横坐标,作出t2-
为横坐标,作出t2- 图线。
图线。
结合上述实验,完成下列任务:
②根据实验步骤(D),可知此单摆的周期为
③该同学根据实验数据,利用计算机作出t2– 图线如图8所示,从理论上分析图线没有过坐标原点的原因,下列分析正确的是 ( )
图线如图8所示,从理论上分析图线没有过坐标原点的原因,下列分析正确的是 ( )
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点开始计时;
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数;
C.不应作t2– 图线,而应作t–
图线,而应作t– 图线;
图线;
D.不应作t2– 图线,而应作t2–(
图线,而应作t2–( +
+ d)图线。
d)图线。
(1)① 1.62 ② 2t/(n-1) ③ D
解析试题分析:①由图示游标卡尺可知,主尺示数是1.6cm,游标尺示数是2×0.1mm=0.2mm=0.02cm,
游标卡尺示数即小球的直径d=1.6cm+0.02cm=1.52cm。
②让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时,并计数为1,此后小球每经过最低点一次,依次计数2、 3……。当数到 n时,此单摆的周期为2t/(n-1)。
③A、B两种做法不会影响图象是不过原点,故A、B错误;t –l是一条曲线,故C错误;单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,摆长小于实际摆长,t2-l图象不过原点,在纵轴上截距不为零,故D正确,故选D。
考点:用单摆测定重力加速度

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案某同学在“研究平抛物体的运动”的实验中,通过描点法画出小球平抛运动的轨迹,并求出小球平抛运动的初速度和抛物线方程。他先调整斜槽轨道使槽口末端水平,然后在方格纸上建立好直角坐标系xOy,将方格纸上的坐标原点O与小球在轨道槽口末端的球心重合,Oy轴与重锤线重合,Ox轴水平(如图甲)。实验中使小球每次都从斜槽同一高度由静止滚下,经过一段水平轨道后抛出。依次均匀下移水平挡板的位置,分别得到小球在挡板上的落点,并在方格纸上标出相应的点迹,再用平滑曲线将方格纸上的点迹连成小球的运动轨迹(如图乙所示)。已知方格边长为L=5cm,重力加速度为g=10m/s2,计算结果取两位有效数字。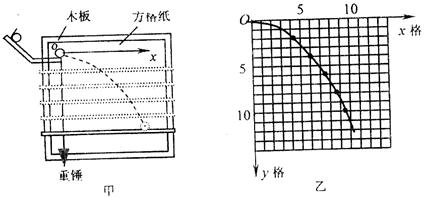
(1)小球平抛的初速度v0= 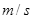 ;
;
(2)小球运动的轨迹方程的表达式为y= x2。
(3)下列哪些说法是正确的
| A.使斜槽末端的切线保持水平 |
| B.每次使小球从不同的高度滚下 |
| C.钢球与斜槽间的摩擦使实验的误差增大 |
| D.计算V0时,所选择的点应离坐标原点稍远些 |


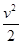 -h图象如图,则当地的重力加速度g=________m/s2。
-h图象如图,则当地的重力加速度g=________m/s2。




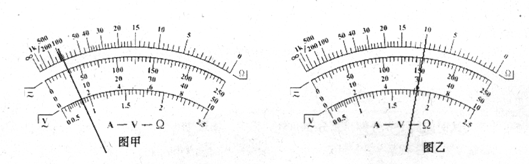
 倍率,用正确的操作方法进行测量,发现指针转过角度太小(如图甲)。为了较准确地进行测量,____应换成么石一倍率的档位进行测量;进行欧姆档调零,将待.测电阻接在两表笔之间,待指针稳定后读数,若这时刻度盘上的指针位置如图乙所示,那么测量结果为____
倍率,用正确的操作方法进行测量,发现指针转过角度太小(如图甲)。为了较准确地进行测量,____应换成么石一倍率的档位进行测量;进行欧姆档调零,将待.测电阻接在两表笔之间,待指针稳定后读数,若这时刻度盘上的指针位置如图乙所示,那么测量结果为____