题目内容
5.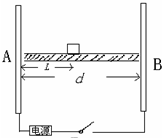 如图所示,相距为d的平行金属板A、B竖直放置,在两板之间水平放置一绝缘平板.有一质量m、电荷量q(q>0)的小物块在与金属板A相距L处静止.若某一时刻在金属板A、B间加一电压,小物块与金属板只A发生了一次碰撞,碰撞后电荷量变为-$\frac{q}{2}$,并以与碰前大小相等的速度反方向弹回.已知小物块与绝缘平板间的动摩擦因素为μ,若不计小物块电荷量对电场的影响和碰撞时间.则:
如图所示,相距为d的平行金属板A、B竖直放置,在两板之间水平放置一绝缘平板.有一质量m、电荷量q(q>0)的小物块在与金属板A相距L处静止.若某一时刻在金属板A、B间加一电压,小物块与金属板只A发生了一次碰撞,碰撞后电荷量变为-$\frac{q}{2}$,并以与碰前大小相等的速度反方向弹回.已知小物块与绝缘平板间的动摩擦因素为μ,若不计小物块电荷量对电场的影响和碰撞时间.则:(1)小物块与金属板A碰撞前瞬间的速度大小是多少?
(2)小物块碰撞后经过多长时间停止运动?停在何位置?
分析 该题的研究情景是电场,能够对小物体进行受力分析,运用牛顿第二定律结合运动学公式求解问题.要注意小物块与A板碰撞时物理量的改变对问题研究的影响.
解答 解:(1)加电压后,由于UAB是负值,所以B极板电势高于A板,电场强度的方向是水平向左.
小物块在电场力作用与摩擦力共同作用下向A板做匀加速直线运动.电场强度为E=$\frac{U}{d}$=$\frac{3μmg}{2q}$;
小物块所受的电场力与摩擦力方向相反,则合外力为 F合=qE-μmg=$\frac{3μmg}{2}$-μmg=$\frac{1}{2}$μmg;
故小物块运动的加速度为a=$\frac{{F}_{合}}{m}$=$\frac{1}{2}$μg
设小物块与A板相碰时的速度为v1,由 v12-0=2a1L,
解得:v1=$\sqrt{μgL}$;
(2)小物块与A板相碰后以v1大小相等的速度反弹,因为电荷量及电性改变,
电场力大小与方向发生变化,摩擦力的方向发生改变,小物块所受的合外力大小为:F合′=μmg+$\frac{qE}{2}$=$\frac{7μmg}{4}$,
加速度大小为a2=$\frac{{F}_{合}′}{m}$=$\frac{7μg}{4}$,
设小物块碰后到停止的时间为 t,注意到末速度为零,有 0-v1=-a2t,解得:t=$\frac{{v}_{1}}{{a}_{2}}$=$\frac{4}{7}\sqrt{\frac{L}{μg}}$,
设小物块碰后停止时距离为x,注意到末速度为零,有 0-v12=-2a2x,解得:x=$\frac{{v}^{2}}{2{a}_{2}}$=2L;
答:(1)小物块与金属板A碰撞前瞬间的速度大小是$\sqrt{μgL}$;
(2)小物块碰撞后经过$\frac{4}{7}$$\sqrt{\frac{L}{μg}}$停止运动,停在2l处或距离A板为2L.
点评 本题考查电场中的动力学问题,受力分析、求合力、求加速度、运用运动学公式求解一些物理量.要注意研究问题的情景随运动过程的改变.

| A. | 作匀速直线运动的物体 | |
| B. | 跳伞运动员从高空跳下打开降落伞后 | |
| C. | 作平抛运动的物体 | |
| D. | 物体在运动过程中不受摩擦力 |
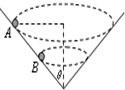 如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则以下说法中正确的是( )
如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则以下说法中正确的是( )| A. | A球的线速度必定小于B球的线速度 | |
| B. | A球的角速度必定小于B球的角速度 | |
| C. | A球的运动周期必定小于B球的运动周期 | |
| D. | A球对筒壁的压力必定等于B球对筒壁的压力 |
| A. | 80J | B. | 800J | C. | 8000J | D. | 400J |
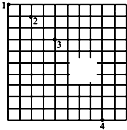 某同学在探究平抛运动的规律实验时,将小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到了如图所示的照片,已知每个小方格边长9.8cm,当地的重力加速度为g=9.8m/s2.
某同学在探究平抛运动的规律实验时,将小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到了如图所示的照片,已知每个小方格边长9.8cm,当地的重力加速度为g=9.8m/s2.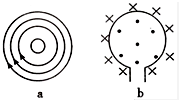
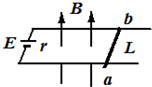 如图所示,水平U形金属导轨(不计金属导轨电阻)的左端接有一个电源,电动势E=1.5V,内阻r=0.4Ω,金属杆ab的电阻R=0.1Ω,质量为m=500g,金属杆ab与导轨组成闭合电路,两条导轨间距L=40cm,导轨区域处于垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T.金属杆ab恰好能够处于静止状态.(g=10m/s2)求:
如图所示,水平U形金属导轨(不计金属导轨电阻)的左端接有一个电源,电动势E=1.5V,内阻r=0.4Ω,金属杆ab的电阻R=0.1Ω,质量为m=500g,金属杆ab与导轨组成闭合电路,两条导轨间距L=40cm,导轨区域处于垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T.金属杆ab恰好能够处于静止状态.(g=10m/s2)求: