题目内容
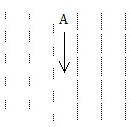 如图中虚线表示某一匀强电场区域内的若干个等势面.质子、氘核、α粒子以相同的初速度,沿与等势面平行的方向由A点进入该电场,从上端进入电场到下端离开电场的过程中,质子、氘核、α粒子的动量改变量之比是
如图中虚线表示某一匀强电场区域内的若干个等势面.质子、氘核、α粒子以相同的初速度,沿与等势面平行的方向由A点进入该电场,从上端进入电场到下端离开电场的过程中,质子、氘核、α粒子的动量改变量之比是1:1:2
1:1:2
,电势能改变量之比是2:1:2
2:1:2
.分析:电场线与等势线垂直,三个粒子进入电场后做类平抛运动,竖直方向做匀速直线运动,水平方向做初速度为0的匀加速运动,运用运动的分解,根据类平抛运动的规律,求出时间的关系,由动量定理求解动量之比.得到偏转距离表达式,电势能的改变量等于电场力做功的多少.
解答:解:根据电场线与等势线垂直,可知,电场线位于水平方向,三个粒子进入进入电场后做类平抛运动,竖直方向做匀速直线运动,水平方向做初速度为0的匀加速运动,则由
t=
,知三个粒子在磁场中运动时间相等.
根据动量定理得:△P=qEt,△P与电荷量成正比,质子、氘核、α粒子的电量之比是1:1:2,则质子、氘核、α粒子的动量改变量之比是1:1:2.
粒子在电场中偏转的距离为y=
at2=
?
(
)2,电势能的改变量△Ep=qEy=
三个粒子的
之比为:2:1:2,则电势能改变量之比是2:1:2.
故答案为:1:1:2,2:1:2.
t=
| L |
| v0 |
根据动量定理得:△P=qEt,△P与电荷量成正比,质子、氘核、α粒子的电量之比是1:1:2,则质子、氘核、α粒子的动量改变量之比是1:1:2.
粒子在电场中偏转的距离为y=
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
| L |
| v0 |
| q2E2L2 | ||
2m
|
三个粒子的
| q2 |
| m |
故答案为:1:1:2,2:1:2.
点评:本题首先要掌握类平抛运动的分解方法,根据动量定理研究动量的变化量,由电势能的改变量等于电场力做功研究电势能的改变量.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目