题目内容
13. 如图所示,体积为V、内壁光滑的圆柱形导热气缸顶部有一质量和厚度均可忽略的活塞,气缸内密封有温度为2.8T0、压强为1.4p0的理想气体.p0和T0分别为大气的压强和温度.已知气体内能U与温度T的关系为U=aT,a为正的常量,容器内气体的所有变化过程都是缓慢的.求
如图所示,体积为V、内壁光滑的圆柱形导热气缸顶部有一质量和厚度均可忽略的活塞,气缸内密封有温度为2.8T0、压强为1.4p0的理想气体.p0和T0分别为大气的压强和温度.已知气体内能U与温度T的关系为U=aT,a为正的常量,容器内气体的所有变化过程都是缓慢的.求①当活塞与顶面间恰好无压力时,气体的温度T;
②最终气体与外界温度相同,则活塞下落过程中气体内能减少了,该过程中气体放出的热量为.
分析 ①当活塞与顶面间恰好无压力时,内部气体压强等于大气压强,结合查理定律求出此时气体的温度.
②根据热力学第一定律求出该过程中放出的热量.
解答 解:①当活塞与顶面间恰好无压力时,气体压强由p1=1.4p0下降到p2=p0,气体的体积不变,温度由T1=2.8T0变为T2=T,
由查理定律得,$\frac{{p}_{1}}{{T}_{1}}=\frac{{p}_{2}}{{T}_{2}}$,
解得T=2T0.
②根据热力学第一定律知,△U=W+Q,
气体内能变化量△U=-a(2T0-T0)=-aT0,
根据盖吕萨克定律得,$\frac{{V}_{2}}{V}=\frac{{T}_{0}}{2{T}_{0}}$,解得${V}_{2}=\frac{1}{2}V$,
则W=${P}_{0}Sd=\frac{1}{2}{P}_{0}V$,
可知Q=-($a{T}_{0}+\frac{{P}_{0}{V}_{0}}{2}$),则放热为($a{T}_{0}+\frac{{P}_{0}{V}_{0}}{2}$).
答:①当活塞与顶面间恰好无压力时,气体的温度T;
②最终气体与外界温度相同,则活塞下落过程中气体内能减少了,该过程中气体放出的热量为($a{T}_{0}+\frac{{P}_{0}{V}_{0}}{2}$).
点评 本题考查了气体定律和热力学第一定律的综合运用,对于第二问,知道气体经历了等压过程的变化,难度不大.

练习册系列答案
相关题目
4.甲乙两队用一根轻绳进行拔河比赛,若轻绳的最大承受力为F,甲队拉绳子的力为F1,乙队拉绳子的力为F2,且甲队取得胜利,则下列说法中正确的是( )
| A. | F1一定大于F2 | B. | F1一定等于F2 | ||
| C. | F1和F2的大小之和一定不能大于F | D. | F1一定不能大于F |
8.如图所示,M是一小型理想变压器,原副线圈匝数比为10:1,接线柱a、b接在电压μ=220$\sqrt{2}$sin100πt(V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,当温度升高时其阻值变小.电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.下列说法正确的是( )


| A. | 副线圈输出的交流电频率为50 Hz | |
| B. | 电压表V1的示数为22$\sqrt{2}$ V | |
| C. | 当传感器R2所在处出现火警时,V1的示数增大,V2的示数增大 | |
| D. | 当传感器R2所在处出现火警时,A1的示数增大,A2的示数增大 |
18. 小船横渡一条两岸平行的河流,船相对于静水的速度大小不变,船身方向垂直于河岸,水流方向与河岸平行,已知小船的运动轨迹如图所示,则( )
小船横渡一条两岸平行的河流,船相对于静水的速度大小不变,船身方向垂直于河岸,水流方向与河岸平行,已知小船的运动轨迹如图所示,则( )
 小船横渡一条两岸平行的河流,船相对于静水的速度大小不变,船身方向垂直于河岸,水流方向与河岸平行,已知小船的运动轨迹如图所示,则( )
小船横渡一条两岸平行的河流,船相对于静水的速度大小不变,船身方向垂直于河岸,水流方向与河岸平行,已知小船的运动轨迹如图所示,则( )| A. | 距离河岸越远,水流速度越小 | B. | 沿图中轨迹渡河时间最短 | ||
| C. | 沿图中轨迹渡河时间最长 | D. | 沿图中轨迹渡河路程最短 |
5.如图(1)所示,理想变压器原、副线圈的匝数比为20:1,R1=10Ω,R2=20Ω,C=100μF 已知电阻R1两端的正弦交流电压如图(2)所示,则( )


| A. | 原线圈输入电压的最大值为400V | B. | 交流电的频率为100Hz | ||
| C. | 电容器C所带电量恒为1×10-3C | D. | 电阻R1消耗的电功率为20W |
3.关于合力与分力,下列说法正确的是( )
| A. | 合力的大小一定大于每一个分力的大小 | |
| B. | 合力的大小至少大于其中一个分力 | |
| C. | 合力的大小可能比两个分力都大,也可能比两个分力都小 | |
| D. | 合力方向可能与其中的一个分力方向垂直 |
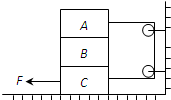 如图所示,质量分别为mA=$\frac{1}{2}$mB=$\frac{1}{3}$mC=1kg的A、B、C三物体叠放在粗糙的水平地面上,各物体间及C物体与地面间的动摩擦因数均为μ=0.1.不计滑轮和绳的质量及其摩擦,若要用力将C物体匀速抽出,则所需拉力的最小值为8N.
如图所示,质量分别为mA=$\frac{1}{2}$mB=$\frac{1}{3}$mC=1kg的A、B、C三物体叠放在粗糙的水平地面上,各物体间及C物体与地面间的动摩擦因数均为μ=0.1.不计滑轮和绳的质量及其摩擦,若要用力将C物体匀速抽出,则所需拉力的最小值为8N.
 如图所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻.有一匀强磁场垂直于导轨平面,磁感应强度为B0=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=2m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻.有一匀强磁场垂直于导轨平面,磁感应强度为B0=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=2m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)