题目内容
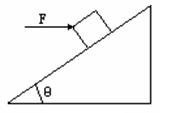
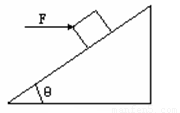
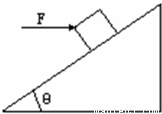
有一个倾角为37°的固定斜面,斜面长l=3.2m,现将一个质量m=1.0kg的物体放在斜面顶端,对物体施加一个沿斜面向上的恒力F作用F=2.4N.物体从静止开始沿斜面匀加速下滑,经过时间2s,物体恰好滑至斜面底端.(1)求物体与斜面间的动摩擦因数;
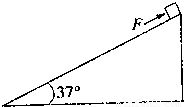
(2)若对物体施加一水平向右的恒力F′,可使物体自斜面底端从静止开始仍经2s匀加速上升回到斜面顶端,问应加多大的水平恒力F′?
(已知sin3°=0.65,cos37°=0.8)
【答案】分析:(1)物体加速下降,根据运动学公式求解加速度,然后受力分析后根据牛顿第二定律列式取决动摩擦因数;
(2)对滑块受力分析,受重力、推力、支持力和滑动摩擦力,根据牛顿第二定律列式求解.
解答:解:(1)加速下降过程中,依牛顿第二定律,有:
mgsin37°-F-μmgcos37°=ma ①
物体匀加速下降,根据位移时间关系公式,有:
l=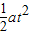 ②
②
由①②解出:μ=0.25 ③
(2)物体加速上升过程中l,t未变,故a不变,
F′cos37°-mgsin37°-μ(F′sin37°+mgcos37°)=ma ④
解出F′=14.8N
答:(1)物体与斜面间的动摩擦因数为0.25;
(2)应加多大的水平恒力F′为14.8N.
点评:本题是已知运动情况确定受力情况的问题,求解出加速度是关键,不难.
(2)对滑块受力分析,受重力、推力、支持力和滑动摩擦力,根据牛顿第二定律列式求解.
解答:解:(1)加速下降过程中,依牛顿第二定律,有:
mgsin37°-F-μmgcos37°=ma ①
物体匀加速下降,根据位移时间关系公式,有:
l=
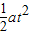 ②
②由①②解出:μ=0.25 ③
(2)物体加速上升过程中l,t未变,故a不变,
F′cos37°-mgsin37°-μ(F′sin37°+mgcos37°)=ma ④
解出F′=14.8N
答:(1)物体与斜面间的动摩擦因数为0.25;
(2)应加多大的水平恒力F′为14.8N.
点评:本题是已知运动情况确定受力情况的问题,求解出加速度是关键,不难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
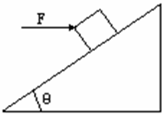 一个倾角为37°的斜面固定不动,其上有一个重10N的物体静止不动,当给物体加一个水平向右的从零逐渐增大到8N的推力作用时物体仍不动下列说法正确的是( )
一个倾角为37°的斜面固定不动,其上有一个重10N的物体静止不动,当给物体加一个水平向右的从零逐渐增大到8N的推力作用时物体仍不动下列说法正确的是( )