题目内容
17.若通过测量纸带上某两点间距离来计算某时刻的瞬时速度,进而验证机械能守恒定律.已知0为第一个点(速度为0)的位置,令2,4两点间距离为s1,0,3两点间距离为s2,打点周期为T(1-4间每一个真实点都取作计数点)打点计时器打下计数点3时,物体的速度表达式V3=$\frac{{S}_{1}}{2T}$;如果0,3两点间机械能守恒,则S1,S2和T应满足的关系为${s}_{1}^{2}$=$8g{S}_{2}{T}^{2}$.分析 纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度.从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答 解:利用匀变速直线运动的推论,打点3时的速度为:
V3=$\frac{{S}_{1}}{2T}$
重物下落的高度h=s2,当机械能守恒时,应有:
mgs2=$\frac{1}{2}$m${v}_{3}^{3}$,
即${S}_{1}^{2}=8g{S}_{2}{T}^{2}$
故答案为:$\frac{{S}_{1}}{2T}$;=$8g{S}_{2}{T}^{2}$
点评 带问题的处理时力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7.某匀强电场方向竖直向上,场强大小为E;一质量为m、带电量为+q的小球以某一初速度竖直向下做匀减速直线运动,其加速度大小为a=$\frac{3qE}{4m}$小球运动距离S时速度变为零.则在此过程中( )
| A. | 电场力做功qES | B. | 小球的电势能增加了$\frac{3}{4}$qES | ||
| C. | 小球的重力势能减少了qES | D. | 物体的动能减少了$\frac{3}{4}$qES |
8.一质点作简谐运动,其位移x与时间t关系曲线如图所示,由图可知( )
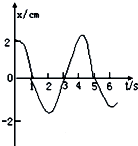

| A. | 质点振动的频率是4Hz | B. | 质点振动的振幅是2cm | ||
| C. | 在t=3s时,质点的速度为正向最大 | D. | 在3s---4s内,质点加速度正向增大 |
5.关于力的概念,下列说法中正确的是( )
| A. | 力不是使物体发生形变和运动状态改变的原因 | |
| B. | 一个力必定联系着两个物体,其中每个物体既是施力物体又是受力物体 | |
| C. | 只要两个力的大小相等,它们产生的效果一定相同 | |
| D. | 两个物体相互作用,其相互作用是有先后的 |
12. 人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度V0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,下列说法正确的是( )
人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度V0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,下列说法正确的是( )
 人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度V0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,下列说法正确的是( )
人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度V0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,下列说法正确的是( )| A. | A物体向上做匀加速运动 | B. | A物体向上做匀减速运动 | ||
| C. | A物体处于超重状态 | D. | 该过程A物体的动能不断减小 |
9.当汽车通过圆弧形凸形桥时,下列说法中正确的是( )
| A. | 汽车在通过桥顶时,对桥的压力大于汽车的重力 | |
| B. | 汽车在通过桥顶时,速度越小,对桥的压力就越小 | |
| C. | 汽车所需的向心力由汽车的重力来提供 | |
| D. | 汽车通过桥顶时,若汽车的速度v=$\sqrt{gR}$(g为重力加速度,R为圆弧形桥面的半径),则汽车对桥顶的压力为零 |
6.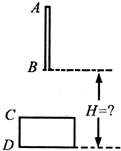 如图所示,一直杆AB长3.8m,从某处自由下落,完全通过高为1m(即CD长为1m)的窗口CD所用时间为0.4s.求:直杆AB的下端B是从距窗台D多高处开始下落的?(不计空气阻力,g取10m/s2)
如图所示,一直杆AB长3.8m,从某处自由下落,完全通过高为1m(即CD长为1m)的窗口CD所用时间为0.4s.求:直杆AB的下端B是从距窗台D多高处开始下落的?(不计空气阻力,g取10m/s2)
 如图所示,一直杆AB长3.8m,从某处自由下落,完全通过高为1m(即CD长为1m)的窗口CD所用时间为0.4s.求:直杆AB的下端B是从距窗台D多高处开始下落的?(不计空气阻力,g取10m/s2)
如图所示,一直杆AB长3.8m,从某处自由下落,完全通过高为1m(即CD长为1m)的窗口CD所用时间为0.4s.求:直杆AB的下端B是从距窗台D多高处开始下落的?(不计空气阻力,g取10m/s2)
7.万有引力定律是下列哪位科学家发现的( )
| A. | 开普勒 | B. | 牛顿 | C. | 伽利略 | D. | 哥白尼 |