题目内容
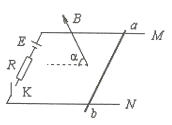
【题目】如图所示，竖直平行正对放置的带电金属板A、B，B板中心的小孔正好位于平面直角坐标系xOy的O点；y轴沿竖直方向；在x>0的区域内存在沿y轴正方向的匀强电场，电场强度大小为
；比荷为1×105 C/kg的带正电的粒子P从A板中心
处静止释放，其运动轨迹恰好经过M（
，1）点；粒子P的重力不计，试求：
（1）金属板AB之间的电势差UAB；
（2）若在粒子P经过O点的同时，在y轴右侧匀强电场中某点由静止释放另一带电微粒Q，使PQ恰能运动中相碰；假设Q的质量是P的2倍、带电情况与P相同；Q的重力及PQ之间的相互作用力均忽略不计；求粒子Q所有释放点的集合。
【答案】（1）1000 V （2）
其中x>0
【解析】
（1）粒子从O点进入右侧匀强电场的速度
，进入右侧电场做类平抛运动，根据类平抛运动的知识求，再由动能定理求金属板AB间的电势差；（2）由牛顿运动定律及类平抛运动的规律和几何关系可得粒子Q所有释放点的集合
（1）设粒子P的质量为m、带电荷量为q，从O点进入匀强电场时的速度大小为；由题意可知，粒子P在y轴右侧匀强电场中做类平抛运动；设从O点运动到M（
，1）点历时为
，由类平抛运动可得：
，
，解得
，
在金属板AB之间，由动能定理：
，解得UAB=1000V；
（2）设PQ在右侧电场中运动的加速度分别为
；Q粒子从坐标N（x，y）点释放后，经时间t与粒子P相遇；由牛顿运动定律及类平抛运动的规律和几何关系可得：
对于P：
，对于Q：
，
，
解得，其中
，
即粒子Q释放点N（x，y）坐标满足的方程为：其中x>0
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
