题目内容
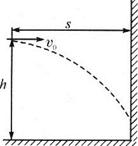
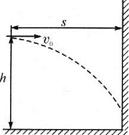
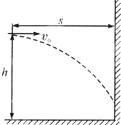 如图所示,小球从离地h=5m高,离竖直墙水平距离s=4m处水平抛出,不计空气阻力,(取g=10m/s2)则:
如图所示,小球从离地h=5m高,离竖直墙水平距离s=4m处水平抛出,不计空气阻力,(取g=10m/s2)则:(1)若要使小球碰不到墙,则它的初速度应满足什么条件?
(2)若以v0=8m/s的初速度向墙水平抛出小球,碰撞点离地面的高度是多少?
分析:(1)小球做平抛运动,若碰不到墙,竖直方向位移为5m,水平方向位移不大于4m,根据平抛运动的分位移公式列式求解即可;
(2)先根据水平分位移公式求解运动时间,再根据竖直分位移公式求解下降的高度.
(2)先根据水平分位移公式求解运动时间,再根据竖直分位移公式求解下降的高度.
解答:解:(1)若小球恰好落到墙角,根据平抛运动的规律,有:
s=vt
h=
gt2
解得:t=
=
=1s
v=
=
=4m/s
(2)若以v0=8m/s的初速度向墙水平抛出小球,则:
运动时间:t1=
=
=0.5s
下落的高度:h1=
g
=
×10×0.25=1.25m
离地高度:h2=h-h1=5-1.25=3.75m
答:(1)若要使小球碰不到墙,则它的初速度应不超过4m/s;
(2)若以v0=8m/s的初速度向墙水平抛出小球,碰撞点离地面的高度是3.75m.
s=vt
h=
| 1 |
| 2 |
解得:t=
|
|
v=
| s |
| t |
| 4m |
| 1s |
(2)若以v0=8m/s的初速度向墙水平抛出小球,则:
运动时间:t1=
| s |
| v0 |
| 4m |
| 8m/s |
下落的高度:h1=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
离地高度:h2=h-h1=5-1.25=3.75m
答:(1)若要使小球碰不到墙,则它的初速度应不超过4m/s;
(2)若以v0=8m/s的初速度向墙水平抛出小球,碰撞点离地面的高度是3.75m.
点评:本题关键是明确小球的运动性质,然后根据平抛运动的分位移公式列式求解,基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
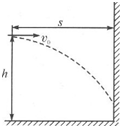 如图所示,小球从离地h=5m高、离竖直墙水平距离s=4m处,以v0=8m/s的初速度向墙水平抛出,不计空气阻力,则(取g=10m/s2)
如图所示,小球从离地h=5m高、离竖直墙水平距离s=4m处,以v0=8m/s的初速度向墙水平抛出,不计空气阻力,则(取g=10m/s2)