题目内容
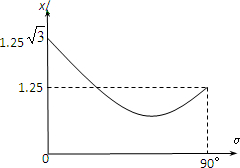 一物体以一定的初速沿斜面向上运动,设它沿斜面向上能达到的最大位移为x.若斜面倾角不同时对应的最大位移x与斜面倾角α的关系如图所示,α可在0°~90°之间变化(g=10m/s2).求:
一物体以一定的初速沿斜面向上运动,设它沿斜面向上能达到的最大位移为x.若斜面倾角不同时对应的最大位移x与斜面倾角α的关系如图所示,α可在0°~90°之间变化(g=10m/s2).求:(1)根据α=0°和α=90°得到的x的特殊值,能够得到哪些有用的结论?
(2)当α=60°时,物体到达最高点后,又回到出发点时,物体速度为多少?
(3)当α为多大时,x有最小值?这最小值为多大?
分析:(1)物体沿斜面向上做匀减速直线运动,由牛顿第二定律和运动学结合,分别得出0°和90°时物体沿斜面上升的最大位移s与斜面倾角θ的关系表达式,即可求出动摩擦因数和初速度;
(2)先求出α=60°时物体上升的高度,然后由动能定理求出物体返回时的速度;
(3)由动能定理得到x与θ的关系式,运用数学知识求解最小值及达到最小值的条件.
(2)先求出α=60°时物体上升的高度,然后由动能定理求出物体返回时的速度;
(3)由动能定理得到x与θ的关系式,运用数学知识求解最小值及达到最小值的条件.
解答:解:(1)当α=90°时,物体做竖直上抛运动,2g (1.25
)=
,得到v0=5m/s;
当α=0°时,由2a(1.25
)=
和a=μg,可得:μ=
;
(2)当α=60°时,物体上向滑行过程中,mgsin60°+μmgcos60°=ma1;
得到a1=
m/s2,则物体上行的最大距离为x=
=
m;
物体下滑过程中,mgsin60°-μmgcos60°=ma2,得到a2=
m/s2;
物体回到出发点时速度为:v2=2 a2x=
,v=
m/s;
(3)对某一角度α,物体上向滑行过程中,mgsinα+μmgcosα=ma,
加速度a=g(sinα+μcosα);
上行的最大距离为x=
=
;
根据辅助角公式:asinα+bcosα=
sin(α+φ),其中tanφ=
,
可以得到:tanφ=μ=
,φ=30°和sinα+μcosα=
sin(α+30°);
当α=60°时,sin(α+30°)=1,x=
最小,代入v和μ的值,x=
m最小.
答:(1)根据α=0°和α=90°得到的x的特殊值,能够得到动摩擦因素和初速度;
(2)当α=60°时,物体到达最高点后,又回到出发点时,物体速度为
m/s;
(3)当α为60°时,x有最小值,这最小值为
m.
| 3 |
| v | 2 0 |
当α=0°时,由2a(1.25
| 3 |
| v | 2 0 |
| ||
| 3 |
(2)当α=60°时,物体上向滑行过程中,mgsin60°+μmgcos60°=ma1;
得到a1=
| 20 |
| 3 |
| 3 |
| ||
| 2a1 |
| 5 |
| 8 |
| 3 |
物体下滑过程中,mgsin60°-μmgcos60°=ma2,得到a2=
| 10 |
| 3 |
| 3 |
物体回到出发点时速度为:v2=2 a2x=
| 25 |
| 2 |
| 5 |
| 2 |
| 2 |
(3)对某一角度α,物体上向滑行过程中,mgsinα+μmgcosα=ma,
加速度a=g(sinα+μcosα);
上行的最大距离为x=
| ||
| 2a |
| ||
| 2g(sinα+μcosα) |
根据辅助角公式:asinα+bcosα=
| a2+b2 |
| b |
| a |
可以得到:tanφ=μ=
| ||
| 3 |
| 1+μ2 |
当α=60°时,sin(α+30°)=1,x=
| ||
2a
|
| 5 |
| 8 |
| 3 |
答:(1)根据α=0°和α=90°得到的x的特殊值,能够得到动摩擦因素和初速度;
(2)当α=60°时,物体到达最高点后,又回到出发点时,物体速度为
| 5 |
| 2 |
| 2 |
(3)当α为60°时,x有最小值,这最小值为
| 5 |
| 8 |
| 3 |
点评:本题关键是根据动能定理求出位移的一般表达式,然后结合图象求出初速度和动摩擦因素,再用解析法求出位移的最小值.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 一物体以一定的初速沿斜面向上运动,设它沿斜面向上能达到的最大位移为x.若斜面倾角不同时对应的最大位移x与斜面倾角α的关系如图所示,α可在0°~90°之间变化(g=10m/s2).求:
一物体以一定的初速沿斜面向上运动,设它沿斜面向上能达到的最大位移为x.若斜面倾角不同时对应的最大位移x与斜面倾角α的关系如图所示,α可在0°~90°之间变化(g=10m/s2).求: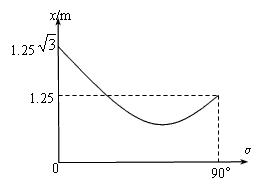
















 g
g
 。
。





