题目内容
【题目】如图,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一质量为m的小球P,横杆右边用一根细线吊一相同的小球Q。当小车沿水平面做变速运动时,细线保持与竖直方向的夹角为α.已知θ<α,不计空气阻力,重力加速度为g,则下列说法正确的是
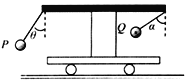
A.小车一定向右做匀加速运动
B.轻杆对小球P的的弹力一定沿轻杆方向
C.小球P受到的合力一定沿水平方向
D.小球Q受到的合力大小为mgtanα
【答案】CD
【解析】
A.对细线吊的小球研究,根据牛顿第二定律:mgtanα=ma,解得:
a=gtanα,
故加速度向右,小车向右加速运动,或向左减速运动,故A错误;
B.由牛顿第二定律:mgtanβ=ma′,因为a=a′,得到:
β=α>θ,
则轻杆对小球的弹力方向与细线平行,故B错误;
CD.小球P和Q的加速度相同,水平向右,则两球的合力均水平向右,大小:
F合=ma=mgtanα,
故CD正确。
故选CD。

练习册系列答案
相关题目