题目内容
11.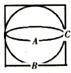 如图所示是一个密闭的内外壁均光滑的薄壁球形容器,质量为m,该球形容器刚好能放入边长为2R的立方体容器中,在金属球壳与立方体的前方、下方、右方三个接触点间安置大小可忽略的压力传感器A、B、C,传感器可以测量球形容器与立方体之间的压力大小,其中A和C处于过球心的水平圆周面上,B和C处于过球心的竖直圆周平面上.容器内有一个质量也为m的可视为质点的小球在运动.通过一段时间的观察,发现传感器A的示数一直为零,B和C的示数随时间周期性变化,若B的最大示数为4mg,则C的最大示数为( )
如图所示是一个密闭的内外壁均光滑的薄壁球形容器,质量为m,该球形容器刚好能放入边长为2R的立方体容器中,在金属球壳与立方体的前方、下方、右方三个接触点间安置大小可忽略的压力传感器A、B、C,传感器可以测量球形容器与立方体之间的压力大小,其中A和C处于过球心的水平圆周面上,B和C处于过球心的竖直圆周平面上.容器内有一个质量也为m的可视为质点的小球在运动.通过一段时间的观察,发现传感器A的示数一直为零,B和C的示数随时间周期性变化,若B的最大示数为4mg,则C的最大示数为( )| A. | $\frac{2}{3}$mg | B. | $\frac{3}{2}$mg | C. | mg | D. | $\sqrt{2}$mg |
分析 传感器A的示数一直为零,B和C的示数随时间周期性变化,说明小球在通过B和C所在竖直平面内做圆周运动,由牛顿第二定律求出球经过B时的速度,由机械能守恒求出经过C点的速度,再由牛顿第二定律求解C的最大示数.
解答 解:球经过B点时,由牛顿第二定律得:
NB-mg=m$\frac{{v}_{B}^{2}}{R}$
由题意 NB=4mg
从B到C,由机械能守恒得:mgR+$\frac{1}{2}m{v}_{C}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$
在C点,有:NC=m$\frac{{v}_{C}^{2}}{R}$
联立解得:NC=mg
则C的最大示数为mg.
故选:C
点评 本题的关键要判断出小球的运动路线,运用机械能守恒定律和牛顿运动定律结合处理圆周运动动力学问题.

练习册系列答案
相关题目
2.下面有关动能的说法正确的是( )
| A. | 物体只有做匀速运动时,动能才不变 | |
| B. | 物体做自由落体运动时,重力做功,物体的动能增加 | |
| C. | 物体做平抛运动时,水平方向速度不变,动能不变 | |
| D. | 物体的动能变化时,速度不一定变化,速度变化时,动能一定变化 |
16.假设一位同学在某星球上完成自由落体运动实验:让一个质量为2kg的物体从一定高度自由下落了8s,测得在第5s内的位移是18m,下列说法正确的是( )
| A. | 物体在第5s内的平均速度是3.6m/s | |
| B. | 物体在第4.5s时的瞬时速度是18m/s | |
| C. | 该星球表面的自由落体加速度是4.0m/s2 | |
| D. | 物体在这8s内下落的高度是64m |
3.关于磁场和磁感线,下列说法正确的是( )
| A. | 单根磁感线可以描述各点磁场的方向和强弱 | |
| B. | 磁体之间的相互作用是通过磁场发生的 | |
| C. | 磁感线是磁场中客观真实存在的线 | |
| D. | 磁感线总是从磁体的北极出发,到南极终止 |
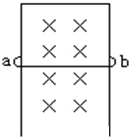 如图所示,有一磁感强度B=0.1T的水平匀强磁场,垂直匀强磁场放置一很长的光滑金属框架,框架上有一导体ab保持与框架边垂直、由静止开始下滑.已知ab长1m,质量为0.1kg,电阻为0.1Ω,框架电阻不计,取g=10m/s2.求:
如图所示,有一磁感强度B=0.1T的水平匀强磁场,垂直匀强磁场放置一很长的光滑金属框架,框架上有一导体ab保持与框架边垂直、由静止开始下滑.已知ab长1m,质量为0.1kg,电阻为0.1Ω,框架电阻不计,取g=10m/s2.求: 某同学为了描绘一个“6V,0.3W”的电学器件的伏安特性曲线,并测出该电学器件在额定电压下的准确电阻值,到实验室寻找到了一些仪器,规格及数量如下:
某同学为了描绘一个“6V,0.3W”的电学器件的伏安特性曲线,并测出该电学器件在额定电压下的准确电阻值,到实验室寻找到了一些仪器,规格及数量如下: 表示)
表示) 如图所示,人通过定滑轮拖住不计重的绳子,将重为G的物体匀速上拉,当人移动d m时,人拉的绳子由竖直方向变为与水平方向成θ角.求这个过程中拉力所做的功.
如图所示,人通过定滑轮拖住不计重的绳子,将重为G的物体匀速上拉,当人移动d m时,人拉的绳子由竖直方向变为与水平方向成θ角.求这个过程中拉力所做的功.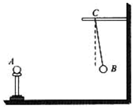 探究两电荷间相互作用力的大小与哪些因素有关的实验中,一同学猜想可能与两电荷的间距和带电量有关.他选用带正电的小球A和B,A球放在可移动的绝缘座上,B球用绝缘丝线悬挂于玻璃棒C点,如图所示.实验时,先保持两球电荷量不变,使A球从远处逐渐向B球靠近,观察到两球距离越小,B球悬线的偏角越大;再保持两球距离不变,改变小球所带的电荷量,观察到电荷量越大,B球悬线的偏角越大.
探究两电荷间相互作用力的大小与哪些因素有关的实验中,一同学猜想可能与两电荷的间距和带电量有关.他选用带正电的小球A和B,A球放在可移动的绝缘座上,B球用绝缘丝线悬挂于玻璃棒C点,如图所示.实验时,先保持两球电荷量不变,使A球从远处逐渐向B球靠近,观察到两球距离越小,B球悬线的偏角越大;再保持两球距离不变,改变小球所带的电荷量,观察到电荷量越大,B球悬线的偏角越大.