题目内容
【题目】第十六届中国崇礼国际滑雪节于2016年12月3日在张家口市崇礼区的长城岭滑雪场隆重进行．如图1所示，跳台滑雪运动员经过一段加速滑行后从A点水平飞出后落到斜坡上的B点，AB两点间的竖直高度h=45m，斜坡与水平面的夹角α=37o ， 不计空气阻力．（取sin37°=0.6，cos37°=0.8；g取10m/s2）求：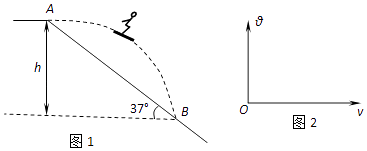
（1）跳台滑雪运动员在空中飞行的时间；
（2）跳台滑雪运动员落到B点时的速度大小；
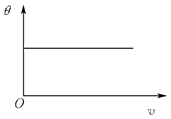
（3）设跳台滑雪运动员从A点以不同的水平速度v飞出落到斜坡上，落到斜坡时的速度与水平方向的夹角为θ，请通过分析在图2中定性画出θ﹣v的关系图象．
【答案】
（1）解：由 
代入数据得：t=3s
答：跳台滑雪运动员在空中飞行的时间是3s；
（2）解：设AB两点间的水平距离为L，则有：L= 
运动员的初速度为：v0= 
联立解得：v0=20m/s
运动员落到B点时竖直的分速度大小为：vy=gt
代入数据得：vy=30m/s
运动员到达B点时的速度大小为： 
m/s
答：跳台滑雪运动员落到B点时的速度大小是10 
/s；
（3）解：设运动员运动过程中的竖直方向位移为h，水平方向位移为：L= ，运动时间由 得：t= 
．
由此得运动员落到斜坡时，速度的水平方向分量为：v= 
，速度的竖直方向分量为：vy=gt= 
设运动员到斜坡时的实际速度与水平方向夹角为θ，则：tanθ= 
=2tanα
由此可说明：速度方向与初速度v无关，只跟斜坡与水平面的夹角α有关．故θ﹣v的关系图象为：
答：如图．
【解析】（1）跳台滑雪运动员在空中做平抛运动，根据下落的高度求飞行的时间；（2）由几何关系求出水平位移的大小，由x=v0t求出水平速度，再合成求得跳台滑雪运动员落到B点时的速度大小；（3）根据速度的分解法求得落到斜坡时的速度与水平方向的夹角与斜面倾角夹角的关系，再画出图象．
【考点精析】通过灵活运用平抛运动，掌握特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动即可以解答此题．
