题目内容
如图12-59所示，MN、PQ是两根足够长固定的平行金属导轨，其间距为L，导轨平面与水平面的夹角为α.在整个导轨平面内都有垂直于导轨平面斜向上方向的匀强磁场，磁感应强度为B，在导轨的M、P端连接一阻值为R的电阻，一根垂直于导轨放置的金属棒ab，质量为m，从静止释放沿导轨下滑，已知ab与导轨间的动摩擦因数为μ.
图12-59
（1）分析ab棒下滑过程中的运动性质，画出其受力示意图.
（2）求ab棒的最大速度.
图12-59
（1）分析ab棒下滑过程中的运动性质，画出其受力示意图.
（2）求ab棒的最大速度.
（1）ab棒做初速为零、加速度逐渐减小的加速运动，当加速度为零时速度最大，最后做匀速直线运动．图见解析.（2）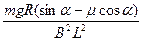
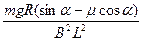
（1）ab下滑做切割磁感线运动，产生的感应电流方向垂直于纸面指向读者，受力如图所示，受到重力mg、支持力N、摩擦力f、安培力F四个力的作用；随着速度的增大，感应电流在增大，安培力也在逐渐增大，而合外力在逐渐减小，加速度就逐渐减小．故ab棒做初速为零、加速度逐渐减小的加速运动，当加速度为零时速度最大，最后做匀速直线运动．
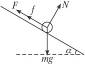
（2）设当棒的速度为v时，感应电动势为E，电路中的电流为I，则E=BLv．
I=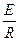
F=BIL
由牛顿第二定律得mgsinα-F-μmgcosα=ma．
解得：a=g(sinα-μcosα)-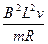
当加速度为零时速度最大，设为vm，则vm=．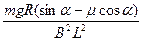
（2）设当棒的速度为v时，感应电动势为E，电路中的电流为I，则E=BLv．
I=
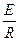F=BIL由牛顿第二定律得mgsinα-F-μmgcosα=ma．
解得：a=g(sinα-μcosα)-
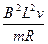
当加速度为零时速度最大，设为vm，则vm=
．
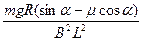练习册系列答案
高中必刷题系列答案
相关题目
，水平放置的平行金属导轨P、Q与金属板C、D接触良好，且导轨在磁感应强度为B1＝10T的匀强磁场中，导轨间距L＝0.50m．金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动．其速度图像如图(乙)，若规定向右运动速度方向为正方向，从t＝0时刻开始，由C板小孔O处连续不断飘入质量为m＝3.2×10－21kg、电量q＝1.6×10－19C的带正电的粒子(设飘入速度很小，可视为零)．在D板外侧有以MN为边界的匀强磁场B2＝10T，MN与D相距d＝10cm，B1和B2方向如图(甲)所示(粒子重力及其相互作用不计)，求：
