题目内容
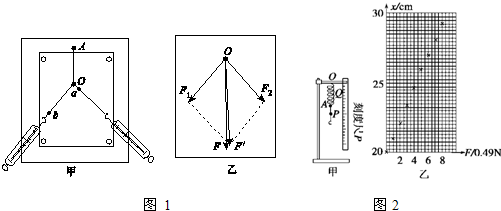
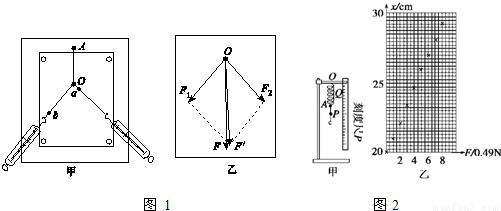
Ⅰ、如图1甲所示,在“验证力的平行四边形定则”的实验中,某同学进行实验的主要步骤是:将橡皮筋的一端固定在木板上的A点,另一端拴上两根绳套,每根绳套分别连着一个弹簧测力计.沿着两个方向拉弹簧测力计,将橡皮筋的活动端拉到某一位置,将该位置标记为O点,读取此时弹簧测力计的示数,分别记录为F1、F2,并用笔在两绳的拉力方向上分别标记a、b两点,分别将其与O点连接,表示两力的方向.再用一个弹簧测力计将橡皮筋的活动端仍拉至O点,记录其拉力F的大小并用上述方法记录其方向.
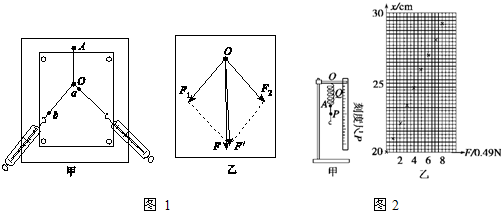
(1)用一个弹簧测力计将橡皮筋的活动端仍拉至O点,这样做的目的是______.
(2)这位同学在实验中确定分力方向时,图1甲所示的a点标记得不妥,其原因是______.
(3)图1乙是在白纸上根据实验结果作出的力的图示,其中______是F1和F2合力的实际测量值.
Ⅱ、“探究弹力和弹簧伸长量的关系”的实验中,选用的螺旋弹簧如图2甲所示.
(1)将弹簧的上端O点固定悬吊在铁架台上,旁边置一刻度尺,刻度尺的零刻线跟O点对齐,在弹簧的下端A处做一标记(如固定一个指针).在弹簧下端的挂钩上挂上钩码(每个钩码的质量都是50g),指针在刻度尺上指示的刻度为x.逐个增加所挂钩码的个数,刻度x随挂钩上的钩码的重量F而变化,几次实验测得相应的 F、x各点已描绘在图2乙中.由图象得出弹簧的劲度系数kA=______N/m.(结果取两位有效数字);此弹簧的弹力大小F跟弹簧伸长量△x的关系是______.
(2)如果将指针固定在A点的下方P处,再作出x随F变化的图象,得出弹簧的劲度系数与kA相比,可能是______
A.大于kA B.等于kA C.小于kA D.无法确定
(3)如果将指针固定在A点的上方Q处,再作出x随F变化的图象,得出弹簧的劲度系数与kA相比,可能是______
A.大于kA B.等于kA C.小于kA D.无法确定.
解:Ⅰ、(1)两次拉到同一位置可以保证前后两次作用力的效果相同;
(2)由图可知,o、a两点距离太近,画力的方向时容易产生误差,应使a离o远一些;
(3)实际测量值一定与AO在同一直线上,而另一合力是由平行四边形得出的,一定为平行四边形的对角线,故F为实际测量值,F′为实验值
Ⅱ、(1)由胡克定律:F=kx可知图象的斜率倒数表示劲度系数,
所以由图象可以解出劲度系数k=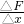 =
=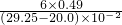 =32N/m
=32N/m
所以弹簧的弹力大小F跟弹簧伸长量△x的关系是F=32△x
(2)如果将指针固定在A点的下方P处,弹簧的劲度系数不变,得出弹簧的劲度系数仍等于kA,故B正确.
(3)如果将指针固定在A点的上方Q处,由于选用的弹簧变短,则弹簧的劲度系数变大,得出弹簧的劲度系数与kA相比,要大于kA,故A正确.
故答案为:Ⅰ、(1)与F1、F2共同作用的效果相同
(2)O、a两点太近,误差大 (3)F
Ⅱ、(1)32,F=32△x
(2)B (3)A
分析:Ⅰ、验证力的平行四边形定则的实验中需要我们让两次拉时的效果相同,且需要记录下拉力的大小及方向;分析两个合力的来源可知实验值及真实值;在找出力的方向时,应使两点距离大一些,这样可以减小误差.
Ⅱ、根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,所以每挂一个钩码拉力增加量相同,弹簧的增加的长度也相同;作图过程中根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,可知画出弹簧弹力F与其伸长量x间关系的F-x图象应为一条倾斜直线.根据F-x图象解斜率即可得到劲度系数.
点评:(1)本题是对基础内容的考查,应注意分析实验的原理及数据处理方法;而最后一问为误差分析,可以根据实验中的要求进行分析.
(2)应用胡克定律注意弹簧的形变量既可以是弹簧的伸长量又可以是压缩量,解题时注意弹簧是被拉长还是被压缩.
(2)由图可知,o、a两点距离太近,画力的方向时容易产生误差,应使a离o远一些;
(3)实际测量值一定与AO在同一直线上,而另一合力是由平行四边形得出的,一定为平行四边形的对角线,故F为实际测量值,F′为实验值
Ⅱ、(1)由胡克定律:F=kx可知图象的斜率倒数表示劲度系数,
所以由图象可以解出劲度系数k=
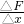 =
=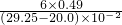 =32N/m
=32N/m所以弹簧的弹力大小F跟弹簧伸长量△x的关系是F=32△x
(2)如果将指针固定在A点的下方P处,弹簧的劲度系数不变,得出弹簧的劲度系数仍等于kA,故B正确.
(3)如果将指针固定在A点的上方Q处,由于选用的弹簧变短,则弹簧的劲度系数变大,得出弹簧的劲度系数与kA相比,要大于kA,故A正确.
故答案为:Ⅰ、(1)与F1、F2共同作用的效果相同
(2)O、a两点太近,误差大 (3)F
Ⅱ、(1)32,F=32△x
(2)B (3)A
分析:Ⅰ、验证力的平行四边形定则的实验中需要我们让两次拉时的效果相同,且需要记录下拉力的大小及方向;分析两个合力的来源可知实验值及真实值;在找出力的方向时,应使两点距离大一些,这样可以减小误差.
Ⅱ、根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,所以每挂一个钩码拉力增加量相同,弹簧的增加的长度也相同;作图过程中根据胡克定律在弹簧的弹性限度内,弹力的大小与弹簧的形变量成正比,可知画出弹簧弹力F与其伸长量x间关系的F-x图象应为一条倾斜直线.根据F-x图象解斜率即可得到劲度系数.
点评:(1)本题是对基础内容的考查,应注意分析实验的原理及数据处理方法;而最后一问为误差分析,可以根据实验中的要求进行分析.
(2)应用胡克定律注意弹簧的形变量既可以是弹簧的伸长量又可以是压缩量,解题时注意弹簧是被拉长还是被压缩.

练习册系列答案
相关题目