题目内容
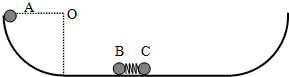 如图所示,光滑固定轨道的两端都是半径为R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,B、C用一长度锁定不变的轻小弹簧栓接,弹性势能Ep=
如图所示,光滑固定轨道的两端都是半径为R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,B、C用一长度锁定不变的轻小弹簧栓接,弹性势能Ep=| 2 | 3 |
(1)弹簧锁定解除前瞬间,D、C速度大小
(2)弹簧锁定解除后,C第一次滑上轨道右侧圆弧部分的轨迹所对的圆心角
(3)弹簧锁定解除后,若C、D(含弹簧)每次碰撞均在水平面;求第N次碰撞结束时,C、D的速度.
分析:1、运用机械能守恒定律求解A球碰撞前的速度,据A、B、C系统动量守恒求解
2、根据弹簧锁定解除前后,系统动量守恒和机械能守恒求解
3、根据C、D(含弹簧)动量守恒和机械能守恒求解
2、根据弹簧锁定解除前后,系统动量守恒和机械能守恒求解
3、根据C、D(含弹簧)动量守恒和机械能守恒求解
解答:解:(1)根据机械能守恒定律得:
mgR=
mv12….①
据A、B、C系统动量守恒得:
mv1=3mv…②
由①②得v=
…③
(2)根据弹簧锁定解除前后,系统动量守恒得:
3mv=mvc+2mvD…④
根据系统机械能守恒得:
3mv2+Ep=
2mvD2+
mvC2…⑤
由③④⑤得:vc=-
(舍去) vc=
vD=-
(舍去) vD=0…⑥
C第一次滑上轨道右侧圆弧部分,根据系统机械能守恒得:
mgR(1-cosθ)=
mvC2…⑦
由⑥⑦得:θ=90°
(3)以左为正方向,根据C、D(含弹簧)动量守恒得:
第一次:mvC=mvC1+2mvD1…⑧
根据系统机械能守恒得:
mgR=
mvC12+
2mvD12…⑨
由⑧⑨得:vC1=
(舍去) vC1=-
vD1=0(舍去) vD1=
….⑩
同理第二次:-2mvD1+mvC1=mvC2+2mvD2…..(11)
mgR=
mvC22+
2mvD22…(12)
由⑩(11)(12)得:vC2=
(舍去) vC2=-
vD2=-
(舍去) vD2=0
综上所述:当N为奇数:vC=
(向右) vD=
当N为偶数时:vC=
(向右) vD=0
答:(1)弹簧锁定解除前瞬间,D、C速度大小是
(2)弹簧锁定解除后,C第一次滑上轨道右侧圆弧部分的轨迹所对的圆心角是90°
(3)弹簧锁定解除后,若C、D(含弹簧)每次碰撞均在水平面,当N为奇数时,CD的速度分别为
(向右)
当N为偶数CD的速度分别为
(向右) vD=0.
mgR=
| 1 |
| 2 |
据A、B、C系统动量守恒得:
mv1=3mv…②
由①②得v=
| ||
| 3 |
(2)根据弹簧锁定解除前后,系统动量守恒得:
3mv=mvc+2mvD…④
根据系统机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由③④⑤得:vc=-
| 1 |
| 3 |
| 2gR |
| 2gR |
| 2 |
| 3 |
| 2gR |
C第一次滑上轨道右侧圆弧部分,根据系统机械能守恒得:
mgR(1-cosθ)=
| 1 |
| 2 |
由⑥⑦得:θ=90°
(3)以左为正方向,根据C、D(含弹簧)动量守恒得:
第一次:mvC=mvC1+2mvD1…⑧
根据系统机械能守恒得:
mgR=
| 1 |
| 2 |
| 1 |
| 2 |
由⑧⑨得:vC1=
| 2gR |
| 1 |
| 3 |
| 2gR |
| 2 |
| 3 |
| 2gR |
同理第二次:-2mvD1+mvC1=mvC2+2mvD2…..(11)
mgR=
| 1 |
| 2 |
| 1 |
| 2 |
由⑩(11)(12)得:vC2=
| 1 |
| 3 |
| 2gR |
| 2gR |
| 2 |
| 3 |
| 2gR |
综上所述:当N为奇数:vC=
| 1 |
| 3 |
| 2gR |
| 2 |
| 3 |
| 2gR |
当N为偶数时:vC=
| 2gR |
答:(1)弹簧锁定解除前瞬间,D、C速度大小是
| ||
| 3 |
(2)弹簧锁定解除后,C第一次滑上轨道右侧圆弧部分的轨迹所对的圆心角是90°
(3)弹簧锁定解除后,若C、D(含弹簧)每次碰撞均在水平面,当N为奇数时,CD的速度分别为
| 1 |
| 3 |
| 2gR |
| 2 |
| 3 |
| 2gR |
当N为偶数CD的速度分别为
| 2gR |
点评:分析清楚A、B、C的运动过程,选择不同的过程应用动量守恒定律和机械能守恒定律,即可正确解题.

练习册系列答案
相关题目
 如图所示,光滑固定导体轨M、N水平放置,两根导体棒P、Q平行放于导轨上,形成一个闭合路,当一条形磁铁从高处下落接近回路时( )
如图所示,光滑固定导体轨M、N水平放置,两根导体棒P、Q平行放于导轨上,形成一个闭合路,当一条形磁铁从高处下落接近回路时( )