题目内容
12. 如图所示,在水平地面上放置一块质量为M的长平板B,在平板的上方某一高度处有一质量为m的物块P由静止开始落下.在平板上方附近存在“相互作用”的区域(如图中虚线所示区域),当物块P进入该区域内,B便会对P产生一个竖直向上的恒力f作用,使得P恰好不与B的上表面接触,且f=kmg,其中k=11.在水平方向上P、B之间没有相互作用力.已知平板与地面间的动摩擦因数μ=2.0×10-3,平板和物块的质量之比$\frac{M}{m}$=10.在P开始下落时,平板B向左运动的速度v0=1.0m/s,P从开始下落到进入相互作用区域经历的时间t0=2.0s.设平板B足够长,保证物块P总能落到B板上方的相互作用区域内,忽略物块P受到的空气阻力,取重力加速度g=10m/s2.求:
如图所示,在水平地面上放置一块质量为M的长平板B,在平板的上方某一高度处有一质量为m的物块P由静止开始落下.在平板上方附近存在“相互作用”的区域(如图中虚线所示区域),当物块P进入该区域内,B便会对P产生一个竖直向上的恒力f作用,使得P恰好不与B的上表面接触,且f=kmg,其中k=11.在水平方向上P、B之间没有相互作用力.已知平板与地面间的动摩擦因数μ=2.0×10-3,平板和物块的质量之比$\frac{M}{m}$=10.在P开始下落时,平板B向左运动的速度v0=1.0m/s,P从开始下落到进入相互作用区域经历的时间t0=2.0s.设平板B足够长,保证物块P总能落到B板上方的相互作用区域内,忽略物块P受到的空气阻力,取重力加速度g=10m/s2.求:(1)物块P从开始下落到再次回到初始位置所经历的时间.
(2)从物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数.
分析 (1)根据自由落体运动的公式求出物体P进入相互作用区域时的速度大小,结合牛顿第二定律求出进入相互作用区域的加速度,通过运动学公式,抓住运动的对称性求出物块P从开始下落到再次回到初始位置所经历的时间.
(2)根据动量定律求出在一个周期内动量的变化量,得出速度的变化量,从而通过整个过程中速度的变化量求出物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数.
解答 解:(1)物块P进入相互作用区域时的速度为V1,则
v1=gt0=20m/s
物块P从进入相互作用区域到速度减小为零的过程中,受到重力和平板的相互作用,设物块在相互作用区域内的下落的加速度为a,根据牛顿第二定律:
kmg-mg=ma
设在相互作用区域内的下落时间为t,根据运动学公式
t=$\frac{{v}_{1}}{a}$
而物块从开始下落到回到初始位置的时间
T=2(t+t0)=$\frac{2k}{k-1}$t0=4.4s.
(2)设在一个运动的周期T内,平板B的速度减小量为△v,根据动量定理有
μMg•2t0+μ(Mg+f)•2t=M△v
解得:
△v=$\frac{2μgk{t}_{0}(1+\frac{m}{M})}{k-1}$=9.7×10-3m/s.
P回到初始位置的次数:
n=$\frac{{v}_{0}}{△v}$=10.3,
n应取整数,即n=10.
答:(1)物块P从开始下落到再次回到初始位置所经历的时间为4.4s.
(2)从物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数为10.
点评 本题综合考查了动量定理、牛顿第二定律、运动学公式等,综合性较强,难度中等,需加强这类题型的训练.

练习册系列答案
相关题目
2.下列关于磁通量的说法中,正确的是( )
| A. | 穿过一个面的磁通量等于磁感应强度与该面面积的乘积 | |
| B. | 在匀强磁场中,穿过某平面的磁通量等于磁感应强度与该面面积的乘积 | |
| C. | 穿过一个面的磁通量就是穿过该面单位面积的磁感线的条数 | |
| D. | 穿过一个面的磁通量就是穿过该面的磁感线的条数 |
20.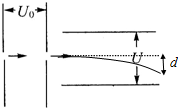 如图,初速为零的电子经加速电场加速后,垂直射入偏转电场,射出时偏转位移为d,若要使d增大些,下列哪些措施是可行的( )
如图,初速为零的电子经加速电场加速后,垂直射入偏转电场,射出时偏转位移为d,若要使d增大些,下列哪些措施是可行的( )
 如图,初速为零的电子经加速电场加速后,垂直射入偏转电场,射出时偏转位移为d,若要使d增大些,下列哪些措施是可行的( )
如图,初速为零的电子经加速电场加速后,垂直射入偏转电场,射出时偏转位移为d,若要使d增大些,下列哪些措施是可行的( )| A. | 增大偏转电场极板间距离 | B. | 增大加速电压U0 | ||
| C. | 增大偏转电压U | D. | 改变偏转电场的场强方向 |
7.如果保持每天仍为24小时,而使地球上物体“漂浮”起来,下面的做法哪一个可达到?(尽管实际作不到)( )
| A. | 增大地球的半径 | B. | 增大地球的自转速度 | ||
| C. | 增大地球的质量 | D. | 减小地球上所有物体的重量 |
17.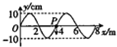 一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )
一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )
 一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )
一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )| A. | 该波沿x轴正方向传播 | |
| B. | 该波的振幅为20cm | |
| C. | 该波的周期为0.4s | |
| D. | 从该时刻起再过0.7s,P点到达波峰的位置 | |
| E. | 从该时刻起再过0.6s,P点沿波的传播方向前进了6m |
4.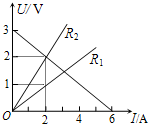 某一电源的路端电压与电流的关系和电阻R1、R2的电压与电流的关系如图所示.用此电源和电阻R1、R2组成电路.R1、R2可以同时接入电路,也可以单独接入电路.则下列说法正确的是.( )
某一电源的路端电压与电流的关系和电阻R1、R2的电压与电流的关系如图所示.用此电源和电阻R1、R2组成电路.R1、R2可以同时接入电路,也可以单独接入电路.则下列说法正确的是.( )
 某一电源的路端电压与电流的关系和电阻R1、R2的电压与电流的关系如图所示.用此电源和电阻R1、R2组成电路.R1、R2可以同时接入电路,也可以单独接入电路.则下列说法正确的是.( )
某一电源的路端电压与电流的关系和电阻R1、R2的电压与电流的关系如图所示.用此电源和电阻R1、R2组成电路.R1、R2可以同时接入电路,也可以单独接入电路.则下列说法正确的是.( )| A. | 将R1、R2串联后接到电源两端时,电源输出功率比将R1、R2单独接到电源两端电源输出功率都小 | |
| B. | 将R1、R2并联后接到电源两端电源输出功率比将R1、R2单独接到电源两端电源输出功率都大 | |
| C. | 将R1单独接到电源两端电源输出功率最大 | |
| D. | 将R2单独接到电源两端电源内部消耗功率为2W |
2.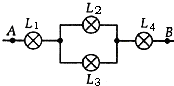 如图所示,灯L1和L2都为“220V 100W“,灯L3和L4都为“220V 40W“.当A、B两点间加上220V的电压时,下列有关说法正确的是( )
如图所示,灯L1和L2都为“220V 100W“,灯L3和L4都为“220V 40W“.当A、B两点间加上220V的电压时,下列有关说法正确的是( )
 如图所示,灯L1和L2都为“220V 100W“,灯L3和L4都为“220V 40W“.当A、B两点间加上220V的电压时,下列有关说法正确的是( )
如图所示,灯L1和L2都为“220V 100W“,灯L3和L4都为“220V 40W“.当A、B两点间加上220V的电压时,下列有关说法正确的是( )| A. | L1最亮 | B. | L2最亮 | C. | L3最亮 | D. | L4最亮 |