题目内容
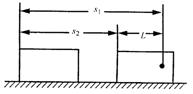
质量为m的子弹,以水平初速度v0射向质量为M的长方体木块。
(1)设木块可沿光滑水平面自由滑动,子弹留在木块内,木块对子弹的阻力恒为f,求弹射入木块的深度L。并讨论:随M的增大,L如何变化?
(2)设v0=900m/s,当木块固定于水平面上时,子弹穿出木块的速度为v1=100m/s。若木块可沿光滑水平面自由滑动,子弹仍以v0=900m/s的速度射向木块,发现子弹仍可穿出木块,求M/m的取值范围(两次子弹所受阻力相同)。
(1) 可打入深度为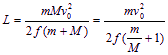 可知,随M增大,L增大。
可知,随M增大,L增大。
(2)M∶m≥80
解析:
(1)当木块可自由滑动时,子弹、木块所组成的系统动量守恒:
![]()
即![]()
可解出打入深度为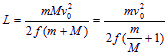 可知,随M增大,L增大。
可知,随M增大,L增大。
(2)当木块固定时:![]() ①
①
![]() ②
②
这种情况下,系统的动能损失仍等于阻力与相对移动距离之积:
![]() ③
③
②③可得:![]() ④
④
由①、④两式![]() ,
,
![]()
可解出![]() ,
,![]() 为子弹刚好穿出时M∶m的值。我们已经知道,M越大,子弹打入木块的深度越大,故M∶m=80应为M∶m的最小值,即应取M∶m≥80。
为子弹刚好穿出时M∶m的值。我们已经知道,M越大,子弹打入木块的深度越大,故M∶m=80应为M∶m的最小值,即应取M∶m≥80。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,质量为2m,长为1的木块置于光滑水平台面上,质量为m的子弹以初速度v0水平向右射向木块,穿出木块时的速度为
如图所示,质量为2m,长为1的木块置于光滑水平台面上,质量为m的子弹以初速度v0水平向右射向木块,穿出木块时的速度为