题目内容
11.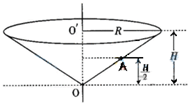 如图所示,一个竖直放置的圆锥筒可绕其中心OO′转动,筒内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半.内壁上有一质量为m的小物块.求
如图所示,一个竖直放置的圆锥筒可绕其中心OO′转动,筒内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半.内壁上有一质量为m的小物块.求(1)当筒不转动时,物块静止在筒壁A点受到的摩擦力和支持力的大小;
(2)当ω=ω0,且其受到的摩擦力为零时,求筒转动的角速度;
(3)请分析当ω=(1+k)ω0与ω=(1-k)ω0时,且0<k<1,小物体均处于静止状态,求小物体分别受到的摩擦力大小和方向.
分析 (1)物体受重力、支持力和静摩擦力,根据平衡条件求解静摩擦力和支持力;
(2)物体受重力和支持力,合力提供向心力,根据平行四边形定则求解出合力,根据向心力公式列式求解筒转动的角速度;
(3)如果物体的角速度ω=(1+k)ω0,物体相对斜面有上滑趋势,静摩擦力平行斜面向下,合力提供向心力,根据牛顿第二定律列式求解静摩擦力;
如果物体的角速度ω=(1-k)ω0,物体相对斜面有下滑趋势,静摩擦力平行斜面向上,合力提供向心力,根据牛顿第二定律列式求解静摩擦力.
解答 解:(1)物体受重力、支持力和静摩擦力,设斜面坡角为θ,根据平衡条件,有:
N=mgcosθ=$\frac{mgR}{\sqrt{{H}^{2}+{R}^{2}}}$
f=mgsinθ=$\frac{mgH}{\sqrt{{H}^{2}+{R}^{2}}}$
(2)当物块在A点随筒做匀速转动,且其所受到的摩擦力为零时,物块在筒壁A点时受到的重力和支持力作用,它们的合力提供向心力,故:
mgtanθ=m${ω}_{0}^{2}r$
其中:
tanθ=$\frac{H}{R}$
r=$\frac{R}{2}$
联立解得:
ω0=$\frac{\sqrt{2gH}}{R}$
(3)如果物体的角速度ω=(1+k)ω0,物体相对斜面有上滑趋势,静摩擦力平行斜面向下,合力提供向心力,根据牛顿第二定律,有:
竖直方向:Ncosθ=mg+fsinθ
水平方向:Nsinθ+fcosθ=mω2r
其中:r=$\frac{R}{2}$
解得:
f=mω2rtanθ-mgsinθ=$m(1+k)^{2}{ω}_{0}^{2}\frac{{R}^{2}}{2\sqrt{{H}^{2}+{R}^{2}}}$-mg$\frac{H}{\sqrt{{H}^{2}+{R}^{2}}}$
如果物体的角速度ω=(1-k)ω0,物体相对斜面有下滑趋势,静摩擦力平行斜面向上,合力提供向心力,根据牛顿第二定律,有:
竖直方向:Ncosθ=mg-fsinθ
水平方向:Nsinθ-fcosθ=mω2r
其中:r=$\frac{R}{2}$
解得:
f=-mω2rtanθ+mgsinθ=-$m{(1-k)}^{2}{ω}_{0}^{2}\frac{{R}^{2}}{2\sqrt{{H}^{2}+{R}^{2}}}$+mg$\frac{H}{\sqrt{{H}^{2}+{R}^{2}}}$
答:(1)当筒不转动时,物块静止在筒壁A点受到的摩擦力为$\frac{mgH}{\sqrt{{H}^{2}+{R}^{2}}}$,支持力的大小为$\frac{mgR}{\sqrt{{H}^{2}+{R}^{2}}}$;
(2)当ω=ω0,且其受到的摩擦力为零时,筒转动的角速度为$\frac{\sqrt{2gH}}{R}$;
(3)当ω=(1+k)ω0时,小物体处于静止状态,小物体受到的摩擦力大小为$m(1+k)^{2}{ω}_{0}^{2}\frac{{R}^{2}}{2\sqrt{{H}^{2}+{R}^{2}}}$-mg$\frac{H}{\sqrt{{H}^{2}+{R}^{2}}}$,方向平行斜面向下.
当ω=(1-k)ω0时,小物体处于静止状态,小物体受到的摩擦力大小为-$m{(1-k)}^{2}{ω}_{0}^{2}\frac{{R}^{2}}{2\sqrt{{H}^{2}+{R}^{2}}}$+mg,方向平行斜面向上.
点评 本题是圆锥摆类型.明确匀速圆周运动中是指向圆心的合力等于向心力,其实是牛顿第二定律的运用,关键是受力分析后根据牛顿第二定律列方程求解.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案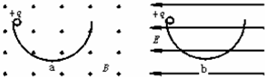 如图所示,两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中,轨道两端在同一高度上,轨道是光滑的而且绝缘,两个相同的带正电小球同时从两轨道左端最高点由静止释放,a、b为轨道的最低点,则正确的是( )
如图所示,两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中,轨道两端在同一高度上,轨道是光滑的而且绝缘,两个相同的带正电小球同时从两轨道左端最高点由静止释放,a、b为轨道的最低点,则正确的是( )| A. | 两小球到达轨道最低点的速度va>vb | |
| B. | 两小球到达轨道最低点时对轨道的压力Fa>Fb | |
| C. | 小球第一次到达a点的时间大于小球第一次到达b点的时间 | |
| D. | 在磁场中小球能到达轨道的另一端,在电场中小球不能到达轨道的另一端 |
| A. | 使物体的质量各减小一半,距离不变 | |
| B. | 使其中一个物体的质量减小到原来的$\frac{1}{4}$,距离不变 | |
| C. | 使两物体间的距离增为原来的4倍,质量不变 | |
| D. | 使两物体间的距离和质量都减为原来的$\frac{1}{4}$ |
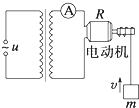 如图所示为一理想变压器,原、副线圈的匝数比为n,原线圈接电压为u=U0sinωt的正弦交流电,输出端接有一个交流电流表和一个电动机,电动机的线圈电阻为R,当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )
如图所示为一理想变压器,原、副线圈的匝数比为n,原线圈接电压为u=U0sinωt的正弦交流电,输出端接有一个交流电流表和一个电动机,电动机的线圈电阻为R,当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )| A. | 电动机两端电压为IR | |
| B. | 原线圈中的电流为nI | |
| C. | 电动机消耗的电功率为$\frac{{U}_{0}I}{n}$ | |
| D. | 重物匀速上升的速度为$\frac{I({U}_{0}-\sqrt{2}nIR)}{\sqrt{2}nmg}$ |
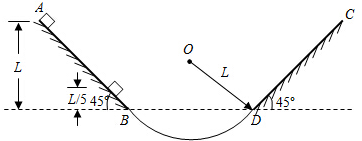
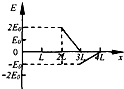
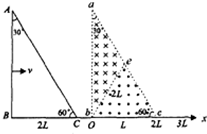 如图所示,有理想边界的直角三角形区域abc内部存在着两个方向相反的垂直纸面的匀强磁场,磁感应强度为B,e是斜边ac上的中点,be是两个匀强磁场的理想分界线.现以b点为原点O,沿直角边bc作x轴,让在纸面内与abc形状完全相同的金属线框ABC的BC边处在x轴上,t=0时导线框C点恰好位于原点0的位置,让ABC沿x轴正方向以恒定的速度v穿过磁场,现规定能产生顺时针方向的电流所对应的感应电动势为正,在下列四个E-x图象中,正确的是(图象中的E0=$\sqrt{3}$BLV)( )
如图所示,有理想边界的直角三角形区域abc内部存在着两个方向相反的垂直纸面的匀强磁场,磁感应强度为B,e是斜边ac上的中点,be是两个匀强磁场的理想分界线.现以b点为原点O,沿直角边bc作x轴,让在纸面内与abc形状完全相同的金属线框ABC的BC边处在x轴上,t=0时导线框C点恰好位于原点0的位置,让ABC沿x轴正方向以恒定的速度v穿过磁场,现规定能产生顺时针方向的电流所对应的感应电动势为正,在下列四个E-x图象中,正确的是(图象中的E0=$\sqrt{3}$BLV)( )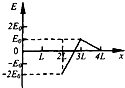
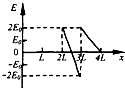
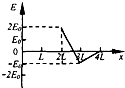
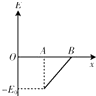
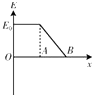
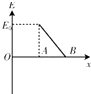
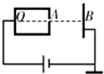 如图所示,金属圆筒左侧接在电源的正极上,电源的负极接在金属板B上(B板接地),AB间为匀强电场.一带负电粒子(重力不计)以某一速度自圆筒 O点经小孔A运动到B板上,则这一过程中带电粒子的电势能E随位置x 变化的图象为( )
如图所示,金属圆筒左侧接在电源的正极上,电源的负极接在金属板B上(B板接地),AB间为匀强电场.一带负电粒子(重力不计)以某一速度自圆筒 O点经小孔A运动到B板上,则这一过程中带电粒子的电势能E随位置x 变化的图象为( )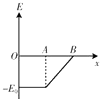
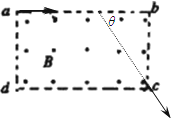 如图所示,矩形abcd范围内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,ab的长度为L=$\frac{\sqrt{3}mv}{2qB}$,现有比荷为$\frac{q}{m}$的正离子从a点沿ab方向射入磁场,刚好从C点飞出,不计正离子的重力.求:
如图所示,矩形abcd范围内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,ab的长度为L=$\frac{\sqrt{3}mv}{2qB}$,现有比荷为$\frac{q}{m}$的正离子从a点沿ab方向射入磁场,刚好从C点飞出,不计正离子的重力.求: