题目内容
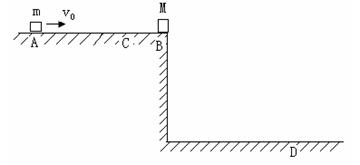
如图所示，一质量为
的滑块静止在水平台面右端
点，另一质量为
的滑块从与点相距
的
点以初速度
以向右运动，至处与发生弹性正碰。碰后沿原路返回至台面
处静止，经时间
落到地面上
点。已知两滑块均能看成质点，且
，点离处的水平距离为
，与台面间的动摩擦因数为
，重力加速度为
，求：
（1）水平台面离地面的高度；
（2）在处的初速度的大小；
（3）点离初始位置的距离。
（1）
（2）
（3）
解析:
（1）设水平台面离地面的高度为
因为碰撞后，
做平抛运动，其竖直方向遵守自由落体规律，所以有：
① 解得 （4分）
（2）设
与碰撞前后瞬间速率分别为
，
，碰后的瞬时速率为
。
因为与发生弹性碰撞，所以有：
② （2分）
③ （2分）
且 
碰后，做平抛运动：
④ （1分）
由④式求得
，代入③④求解得：
，
（方向向左） （1分）
因为碰前做匀减速运动，其加速度大小为
，所以有：
⑤
代入数据求解得： （2分）
（3）碰后，从
向左做匀减速运动，至
处静止，设其位移为
⑥ （2分）
代入数据求解得：
所以点离初始位置
的距离为：
⑦ （2分）
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
的带电小球，用长为
的绝缘细线悬挂在场强大小为E、方向水平向右的匀强电场中，静止时悬线与竖直方向成
角，重力加速度大小为g．
的带电小球，用长为
的绝缘细线悬挂在场强大小为E、方向水平向右的匀强电场中，静止时悬线与竖直方向成
角，重力加速度大小为g．
的物块A与直立轻弹簧的上端连接，弹簧的下端固定在地面上，一质量也为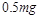
时，A物块上升的高度为L，此过程中，该拉力做的功为
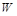；若A、B不粘连，用一竖直向上的恒力
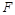作用在B上，当A物块上升的高度也为L时，A、B恰好分离。已知重力加速度为g，不计空气阻力，求：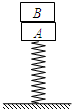
；
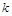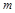的物块A与直立轻弹簧的上端连接，弹簧的下端固定在地面上，一质量也为
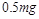时，A物块上升的高度为L，此过程中，该拉力做的功为
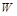；若A、B不粘连，用一竖直向上的恒力
作用在B上，当A物块上升的高度也为L时，A、B恰好分离。已知重力加速度为g，不计空气阻力，求：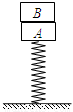
；