题目内容
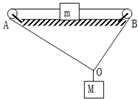 两物体M、m 用跨过光滑定滑轮的轻绳相连,如图放置,OA、OB与水平面的夹角分别为30°、60°,M重20N,M、m均处于静止状态.求:
两物体M、m 用跨过光滑定滑轮的轻绳相连,如图放置,OA、OB与水平面的夹角分别为30°、60°,M重20N,M、m均处于静止状态.求:(1)OA、OB对M的拉力?
(2)m受到的静摩擦力的大小和方向?
分析:(1)先对结点O受力分析,再沿水平方向对正交分解,然后利用平衡条件求出AO、BO绳的张力F1和F2.
(2)对m受力分析,两绳对m的拉力为水平向左的F1,水平向右的F2,由平衡条件知F1和F2的差就等于m受到的摩擦力的大小.
(2)对m受力分析,两绳对m的拉力为水平向左的F1,水平向右的F2,由平衡条件知F1和F2的差就等于m受到的摩擦力的大小.
解答:解:(1)对结点O受力分析如图:

把F1和F2分别分解到水平方向和竖直方向.
沿水平方向列方程:
F1cos30°=F2cos60°…①
沿竖直方向列方程:
F1sin30°+F2sin60°=Mg…②
由①②联立得:
F1=10N,F2=10
N.
(2)对m受力分析如下图:

水平方向列平衡方程:F1+f=F2…③
由③解得:f=F2-F1=(10
-10)N,方向水平向左.
答:(1)OA、OB对M的拉力分别为10N,10
N.
(2)m受到的静摩擦力的大小为(10
-10)N,方向水平向左.

把F1和F2分别分解到水平方向和竖直方向.
沿水平方向列方程:
F1cos30°=F2cos60°…①
沿竖直方向列方程:
F1sin30°+F2sin60°=Mg…②
由①②联立得:
F1=10N,F2=10
| 3 |
(2)对m受力分析如下图:

水平方向列平衡方程:F1+f=F2…③
由③解得:f=F2-F1=(10
| 3 |
答:(1)OA、OB对M的拉力分别为10N,10
| 3 |
(2)m受到的静摩擦力的大小为(10
| 3 |
点评:解决本题的关键能够正确地受力分析,运用共点力平衡进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 两物体M、m 用跨过光滑定滑轮的轻绳相连,如图放置,OA、OB与水平面的夹角分别为30°、60°,物体M的重力大小为20N,M、m均处于静止状态.则下列判断错误的是( )
两物体M、m 用跨过光滑定滑轮的轻绳相连,如图放置,OA、OB与水平面的夹角分别为30°、60°,物体M的重力大小为20N,M、m均处于静止状态.则下列判断错误的是( )A、OA绳的拉力为10
| ||
| B、OB绳的拉力为10N | ||
C、地面对m的摩擦力大小为10
| ||
| D、地面对m的摩擦力方向水平向左 |
 两物体M、m用跨过光滑定滑轮的轻绳相连,如图所示,OA、OB与水平面的夹角分别为30°、60°,M、m均处于静止状态.则( )
两物体M、m用跨过光滑定滑轮的轻绳相连,如图所示,OA、OB与水平面的夹角分别为30°、60°,M、m均处于静止状态.则( )| A、绳OA的拉力大于绳OB的拉力 | B、绳OA的拉力小于绳OB的拉力 | C、m受到水平面的静摩擦力的方向水平向左 | D、m受到水平面的静摩擦力的方向水平向右 |
 (2011?闵行区模拟)如图所示两物体M、m 用跨过光滑定滑轮的轻绳相连,m放在水平面上,M重20N,M、m均处于静止状态,OA、OB与水平面的夹角分别为30°、60°,求:
(2011?闵行区模拟)如图所示两物体M、m 用跨过光滑定滑轮的轻绳相连,m放在水平面上,M重20N,M、m均处于静止状态,OA、OB与水平面的夹角分别为30°、60°,求: 两物体M和m用跨过光滑定滑轮的轻绳相连,如图所示放置,OA,OB与水平面的夹角分别为30°和60°,M重20N,m重15N,且m与台面间的动摩擦因数μ为0.6,求:
两物体M和m用跨过光滑定滑轮的轻绳相连,如图所示放置,OA,OB与水平面的夹角分别为30°和60°,M重20N,m重15N,且m与台面间的动摩擦因数μ为0.6,求: 两物体M、m 用跨过光滑定滑轮的轻绳相连,如图所示放置,OA、OB与水平面的夹角分别为30°、60°,M重20N,M、m均处于静止状态.则下列判断正确的是( )
两物体M、m 用跨过光滑定滑轮的轻绳相连,如图所示放置,OA、OB与水平面的夹角分别为30°、60°,M重20N,M、m均处于静止状态.则下列判断正确的是( )