题目内容
有两个简谐运动的振动方程x1=6sin(100πt+
)，x2=6sin(100πt+
)，则下列说法中错误的是（ ）
| π |
| 6 |
| π |
| 3 |
分析：根据两个简谐运动的振动方程读出位移大小的最大值，即为振幅，读出角速度，求出周期．读出相位，求出其差，分析步调关系．
解答：解：
A、由题，第一简谐运动的振幅为A1=6，第二简谐运动的振幅也为A1=6，所以它们的振幅相同．故A正确．
B、第一简谐运动的角速度为ω1=100πrad/s，其周期为T1=
=0.02s，第二简谐运动的角速度为ω2=100πrad/s，其周期为T2=
=0.02s，周期相同．故B正确．
C、第一简谐运动的相位为φ1=100π+
，第二简谐运动的相位为φ2=100π+
，相差为△φ=φ2-φ1=
，恒定不变．故C正确．
D、由上看出，两个简谐运动存在相位差，步调不一致．故D错误．
本题选错误的，故选D
A、由题，第一简谐运动的振幅为A1=6，第二简谐运动的振幅也为A1=6，所以它们的振幅相同．故A正确．
B、第一简谐运动的角速度为ω1=100πrad/s，其周期为T1=
| 2π |
| ω1 |
| 2π |
| ω2 |
C、第一简谐运动的相位为φ1=100π+
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
D、由上看出，两个简谐运动存在相位差，步调不一致．故D错误．
本题选错误的，故选D
点评：本题考查对振动方程的理解，读取振幅、角速度、相位的基本能力，可根据标准方程x=Asin（ωt+φ0）对照读取．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
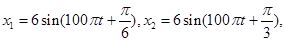则下列说法中正确的是( )
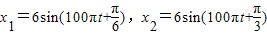，则下列说法中错误的是（ ）
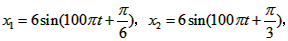则下列说法中错误的是