题目内容
13.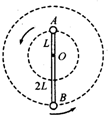 如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑水平转动轴上,杆和球在竖直面内转动,已知球A运动到最高点时,球A的速度刚好为$\sqrt{3gL}$.求:
如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑水平转动轴上,杆和球在竖直面内转动,已知球A运动到最高点时,球A的速度刚好为$\sqrt{3gL}$.求:(1)杆此时对球作用力大小和方向;
(2)杆此时对水平轴O的作用力大小和方向.
分析 (1)小球A在最高点靠重力和杆子的作用力合力提供向心力,结合牛顿第二定律求出杆对球的作用力大小和方向.
(2)抓住A、B的角速度相等,求出B的线速度,结合牛顿第二定律求出杆子对B的作用力大小,从而得出B对杆子的作用力,结合A对杆子的作用力,得出杆对水平轴O的作用力大小和方向.
解答 解:(1)球A在最高点的速度:${v}_{A}=\sqrt{3gL}>\sqrt{gL}$,杆OA对球A的力为拉力,
根据牛顿第二定律得:${F}_{A}+mg=m\frac{{{v}_{A}}^{2}}{L}$,
代入数据得:FA=2mg.
杆OA对球的作用力大小为2mg 方向竖直向下.
(2)球B的受力满足:FB-mg=m$\frac{{{v}_{B}}^{2}}{2L}$,
由于A、B两球共轴转动,由v=rω知:${v}_{B}=2{v}_{A}=2\sqrt{3gL}$,
上两式代入数据得:FB=7mg,方向竖直向上.
由牛顿第三定律知:杆OA对轴O作用力FA′方向竖直向上,大小为2mg.
杆OB对轴的作用力FB′方向竖直向下,大小为7mg.
所以轴O受力大小为:F=FB′-FA′=7mg-2mg=5mg,方向竖直向下.
答:(1)杆此时对球作用力大小为2mg,方向竖直向下.
(2)杆此时对水平轴O的作用力大小为5mg,方向竖直向下.
点评 解决本题的关键知道A、B做圆周运动向心力的来源,知道A、B的角速度相等,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
相关题目
3. 如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )
如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )
 如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )
如图所示,一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点).将其放在一个直角形光滑槽中,已知当轻杆与槽左壁成α角时,B球沿槽上滑的速度为vB,则此时A球的速度vA的大小为( )| A. | vB | B. | $\frac{{v}_{B}}{sinα}$ | C. | vBcotα | D. | vBtanα |
4. 如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )
如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )
 如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )
如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在自发跃迁中放出一些光子,用这些光子照射逸出功为2.25ev的钾,下列说法正确的是( )| A. | 这群氢原子能发出三种不同频率的光 | |
| B. | 这群氢原子发出光子均能使金属钾发生光电效应 | |
| C. | 金属钾表面逸出的光电子最大初动能一定小于12.09ev | |
| D. | 金属钾表面逸出的光电子最大初动能可能等于9.84ev |
18.己知地球同步卫星A离地面的高度约为地球半径的6倍,另一地球卫星B离地面的高度约为地球半径的2.5倍,在地球赤道上放置一物体C,随地球转动.若将地球看成均匀球体,则( )
| A. | 两颗卫星A、B的角速度之比约为1:2$\sqrt{2}$ | |
| B. | 两颗卫星A、B的线速度之比约为1:$\sqrt{2}$ | |
| C. | 卫星B和物体C的向心加速度之比约为1:1 | |
| D. | 卫星A和物体C受到地球的万有引力之比约为1:49 |
5.物理学家通过艰辛的实验和理论研究,探索出自然规律为人类的进步做出巨大贡献,值得我们敬仰,下列表述中符合物理学史的是( )
| A. | 牛顿最早指出力不是维持物体运动的原因 | |
| B. | 伽利略提出了万有引力定律 | |
| C. | 开普勒总结归纳了行星运动定律,从而提出了日心说 | |
| D. | 卡文迪许测出了引力常量 |
 有一质量m=20kg的物体以水平速度v0=5m/s滑上静止在光滑水平面上的平板小车,小车的质量M=80kg,物体在平板小车上相对小车滑行一段距离s=4m后不再滑动,g取10m/s2,求:
有一质量m=20kg的物体以水平速度v0=5m/s滑上静止在光滑水平面上的平板小车,小车的质量M=80kg,物体在平板小车上相对小车滑行一段距离s=4m后不再滑动,g取10m/s2,求: 如图所示,甲车质量m1=10kg,车上有质量M=50kg的人,甲车(连同车上的人)从足够长的斜坡上高h=0.45m处由静止滑下,到水平面上后继续向前滑动,此时质量m2=20kg的乙车正以v0=2m/s的速度迎面滑来,为了避免两车相撞,当两车相距适当距离时,人从甲车跳到乙车上,求人跳出甲车的水平速度(相对地面)应在什么范围内,不计地面和斜坡的摩擦(g=10m/s2)
如图所示,甲车质量m1=10kg,车上有质量M=50kg的人,甲车(连同车上的人)从足够长的斜坡上高h=0.45m处由静止滑下,到水平面上后继续向前滑动,此时质量m2=20kg的乙车正以v0=2m/s的速度迎面滑来,为了避免两车相撞,当两车相距适当距离时,人从甲车跳到乙车上,求人跳出甲车的水平速度(相对地面)应在什么范围内,不计地面和斜坡的摩擦(g=10m/s2)