题目内容
9. 在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴负方向的匀强电场,在其他三个象限存在垂直于坐标平面向外的匀强磁场,电场、磁场均足够大.一带正电的粒子A从y轴上图中的P点以速度v0垂直于y轴射入电场,经电场后从x轴上的Q点,以与x轴正方向成θ=60°角的方向射出电场.当粒子A进入磁场后,在x轴上方即将沿垂直y轴的方向从磁场中射出时,与静放在y轴上的不带电粒子B发生弹性正碰.已知B粒子的质量为A粒子质量的3倍.若A、B碰撞时粒子的质量、电量均不变,粒子的重力不计.试求:粒子A与粒子B碰后第一次射出磁场时的速度.
在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴负方向的匀强电场,在其他三个象限存在垂直于坐标平面向外的匀强磁场,电场、磁场均足够大.一带正电的粒子A从y轴上图中的P点以速度v0垂直于y轴射入电场,经电场后从x轴上的Q点,以与x轴正方向成θ=60°角的方向射出电场.当粒子A进入磁场后,在x轴上方即将沿垂直y轴的方向从磁场中射出时,与静放在y轴上的不带电粒子B发生弹性正碰.已知B粒子的质量为A粒子质量的3倍.若A、B碰撞时粒子的质量、电量均不变,粒子的重力不计.试求:粒子A与粒子B碰后第一次射出磁场时的速度.
分析 粒子在电场中做类平抛运动,求出粒子射入磁场时的速度,粒子A、B发生碰撞时动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律可以求出碰撞后A的速度,然后根据粒子A的运动情况求出粒子离开磁场时的速度.
解答 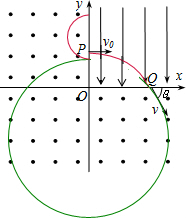 解:粒子在匀强电场中做类平抛运动,粒子进入磁场时的速度为:
解:粒子在匀强电场中做类平抛运动,粒子进入磁场时的速度为:
v=v0cos60°=2v0,
由题意可知,粒子A、B碰撞过程动量守恒、机械能守恒,以A的初速度方向为正方向,由动量守恒定律得:
mv=mvA+3mvB,
由机械能守恒定律得:12mv2=12mvA2+12•3mvB2,
解得:vA=-v0,负号表示A的速度方向与初速度方向相反,水平向左,vB=v0,
碰撞后A的速度反向,在第二象限沿顺时针方向做圆周运动,
经过半个圆周后A离开磁场,速度大小为:v0,方向水平向右.
答:粒子A与粒子B碰后第一次射出磁场时的速度大小为v0,方向水平向右.
点评 本题考查了粒子在电场与磁场中的运动,考查了求粒子的速度,分析清楚粒子运动过程、应用速度的合成与分解、动量守恒定律与机械能守恒定律可以解题;分析清楚粒子运动过程是正确解题的关键.

练习册系列答案
相关题目
11.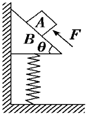 如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直粗糙墙壁,处于静止状态.现用力F沿斜面向上推A,A、B仍处于静止状态.下列说法正确的是( )
如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直粗糙墙壁,处于静止状态.现用力F沿斜面向上推A,A、B仍处于静止状态.下列说法正确的是( )
 如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直粗糙墙壁,处于静止状态.现用力F沿斜面向上推A,A、B仍处于静止状态.下列说法正确的是( )
如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直粗糙墙壁,处于静止状态.现用力F沿斜面向上推A,A、B仍处于静止状态.下列说法正确的是( )| A. | A、B之间的摩擦力大小可能不变 | B. | A、B之间的摩擦力一定变小 | ||
| C. | B受到的弹簧弹力一定变小 | D. | B与墙之间可能没有摩擦力 |
12.一列简谐横波沿x轴传播,t=0时刻的波形如图所示.则从图中可以看出( )
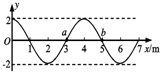

| A. | 这列波的波长为4m | |
| B. | 波中的每个质点的振动周期为5s | |
| C. | 若已知波沿x轴正向传播,则此时质点a向下振动 | |
| D. | 若已知质点b此时向上振动,则波是沿x轴负向传播的 |
9.我国于2007年成功发射“嫦娥一号”月球探测卫星并对月球进行了扫描拍照,2009年3月,完成科学探测任务的嫦娥一号卫星在控制下成功撞击月球.用d表示月球的直径,g表示月球表面重力加速度,则下列说法中正确的是( )
| A. | “嫦娥一号”环绕月球做圆周运动的速度大于√dg2 | |
| B. | “嫦娥一号”绕月球一周的时间不少于π√2dg | |
| C. | 要使轨道上的“嫦娥一号”撞击月球,应先让它减速 | |
| D. | “嫦娥一号”撞向月球的过程中,卫星上的工作器材处于超重状态 |
1.太阳系原有九大行星,它们均绕太阳旋转.2006年,国际天文学大会重新对太阳系的天体进行了严格的定义,把绕太阳运转的天体分为行星、矮行星和太阳系小天体,这使得冥王星被降级为矮行星,太阳系则变为拥有八大行星.下列说法正确的是( )
| A. | 冥王星绕太阳公转的轨道平面一定通过太阳中心 | |
| B. | 冥王星绕太阳公转的轨道平面可能不通过太阳中心 | |
| C. | 冥王星绕太阳公转的周期一定大于一年 | |
| D. | 冥王星被降级为矮行星后不再绕太阳运转 |
19.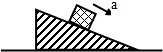 如图所示,粗糙水平地面上有一斜劈,斜劈上一物块正在沿斜面以加速度a匀加速下滑,物块质量为m,下滑过程斜劈始终保持不动,下列说法正确的是( )
如图所示,粗糙水平地面上有一斜劈,斜劈上一物块正在沿斜面以加速度a匀加速下滑,物块质量为m,下滑过程斜劈始终保持不动,下列说法正确的是( )
 如图所示,粗糙水平地面上有一斜劈,斜劈上一物块正在沿斜面以加速度a匀加速下滑,物块质量为m,下滑过程斜劈始终保持不动,下列说法正确的是( )
如图所示,粗糙水平地面上有一斜劈,斜劈上一物块正在沿斜面以加速度a匀加速下滑,物块质量为m,下滑过程斜劈始终保持不动,下列说法正确的是( )| A. | 增大物块质量m,物块加速度变大,斜劈受地面摩擦力不变 | |
| B. | 增大物块质量m,物块加速度不变,斜劈受地面摩擦力变大 | |
| C. | 竖直向下对物块施加一压力F,物块加速度变大,斜劈受地面摩擦力变大 | |
| D. | 平行斜面对物块施加一向下推力F,物块加速度变大,斜劈受到地面的摩擦力变大 |
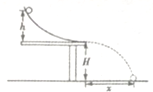 某同学利用如图所示的实验装置验证机械能守恒定律.桌面离地面的高度为H,将钢球从轨道的不同高度h处由静止释放,钢球的落点距轨道末端的水平距离为x.
某同学利用如图所示的实验装置验证机械能守恒定律.桌面离地面的高度为H,将钢球从轨道的不同高度h处由静止释放,钢球的落点距轨道末端的水平距离为x.