题目内容
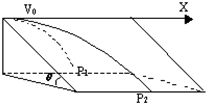 a、b两质点从同一点O分别以相同的水平速度v沿x轴正方向抛出,a在竖直平面内运动,落地点为P1,b沿光滑斜面运动,落地点为P2,P1和P2在同一水平面上,如图所示,不计空气阻力,则下列说法中正确的是( )
a、b两质点从同一点O分别以相同的水平速度v沿x轴正方向抛出,a在竖直平面内运动,落地点为P1,b沿光滑斜面运动,落地点为P2,P1和P2在同一水平面上,如图所示,不计空气阻力,则下列说法中正确的是( )分析:小球A做平抛运动,小球B做类平抛运动,结合下落的高度求出运动的时间,进行比较.通过初速度和运动的时间比较沿x轴方向上的位移.求出落地时的速度,从而比较大小.
解答:解:A、对于A球,根据h=
gta2得,ta=
.对于B球,在沿斜面向下方向上有:
=
gsinθtb2,解得tb=
,可知tb>ta.故A错误.
B、在x轴方向上,有x=v0t,知b沿x轴的位移大于a沿x轴的位移.故B错误.
C、根据动能定理得,因为只有重力做功,且重力做功和初动能相等,则末动能相等,所以a、b落地时的速度大小相等,速度方向不同.故C正确,D错误.
故选C.
| 1 |
| 2 |
|
| h |
| sinθ |
| 1 |
| 2 |
|
B、在x轴方向上,有x=v0t,知b沿x轴的位移大于a沿x轴的位移.故B错误.
C、根据动能定理得,因为只有重力做功,且重力做功和初动能相等,则末动能相等,所以a、b落地时的速度大小相等,速度方向不同.故C正确,D错误.
故选C.
点评:解决本题的关键掌握处理类平抛运动的方法,通过水平方向和沿斜面向下方向的规律进行分析求解.对于D选项,也可以通过动能定理进行分析.

练习册系列答案
相关题目
 A、B两质点从同一点开始沿直线运动,右图中的①、②分别为二者的υ-t图线,则下列判断中正确的是( )
A、B两质点从同一点开始沿直线运动,右图中的①、②分别为二者的υ-t图线,则下列判断中正确的是( ) 如图是A、B两质点从同一点出发的速度-时间图象,由图象可知( )
如图是A、B两质点从同一点出发的速度-时间图象,由图象可知( ) (2012?卢湾区一模)A、B两质点从同一点开始沿直线运动,右图中的①、②分别为二者的υ-t图线,则下列判断中正确的是( )
(2012?卢湾区一模)A、B两质点从同一点开始沿直线运动,右图中的①、②分别为二者的υ-t图线,则下列判断中正确的是( )