题目内容
11. 如图所示,AB和CD是足够长的平行光滑导轨,其间距为L,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,.AC端连有电阻值为R的电阻.若将一质量为M、电阻为r的金属棒EF垂直于导轨在距BD端s处由静止释放,在棒EF滑至底端前会有加速和匀速两个运动阶段.今用大小为F,方向沿斜面向上的恒力把棒EF从BD位置由静止推至距BD端s处,突然撤去恒力F,棒EF最后又回到BD端.(导轨的电阻不计)
如图所示,AB和CD是足够长的平行光滑导轨,其间距为L,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,.AC端连有电阻值为R的电阻.若将一质量为M、电阻为r的金属棒EF垂直于导轨在距BD端s处由静止释放,在棒EF滑至底端前会有加速和匀速两个运动阶段.今用大小为F,方向沿斜面向上的恒力把棒EF从BD位置由静止推至距BD端s处,突然撤去恒力F,棒EF最后又回到BD端.(导轨的电阻不计)(1)求棒EF下滑过程中的最大速度;
(2)求恒力F刚推棒EF时棒的加速度;
(3)棒EF自BD端出发又回到BD端的整个过程中,电阻R上有多少电能转化成了内能?
分析 (1)当棒子的加速度为零时,棒的速度最大.根据共点力平衡求出EF下滑的最大速度.
(2)根据牛顿第二定律求出恒力F刚推棒EF时棒的加速度.
(3)棒先向上减速至零,然后从静止加速下滑,在滑回BD之前已达最大速度vm开始匀速,结合能量守恒定律求出EF自BD端出发又回到BD端的整个过程中,电阻R上消耗的电能.
解答 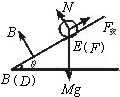 解:(1)如图所示,当EF从距BD端s处由静止开始滑至BD的过程中,受力情况如图所示.安培力:F安=BIL=B$•\frac{BLv}{R+r}L$.
解:(1)如图所示,当EF从距BD端s处由静止开始滑至BD的过程中,受力情况如图所示.安培力:F安=BIL=B$•\frac{BLv}{R+r}L$.
根据牛顿第二定律:Mgsinθ-F安=Ma
当a=0时速度达到最大值vm,即:vm=$\frac{Mg(R+r)sinθ}{{B}^{2}{L}^{2}}$.
(2)根据牛顿第二定律:F-Mgsinθ=Ma
得 $a=\frac{F-Mgsinθ}{M}$
(3)棒先向上减速至零,然后从静止加速下滑,在滑回BD之前已达最大速度vm开始匀速.
设EF棒由BD从静止出发到再返回BD过程中,转化成的内能为△E.根据能的转化与守恒定律:
Fs-△E=$\frac{1}{2}$Mvm2
△E=$Fs-\frac{1}{2}$M[$\frac{Mg(R+r)sinθ}{{B}^{2}{L}^{2}}$]2
△ER=$\frac{R}{R+r}Fs-$$\frac{RM}{2(R+r)}$[$\frac{Mg(R+r)sinθ}{{B}^{2}{L}^{2}}$]2
答:(1)棒EF下滑过程中的最大速度为$\frac{Mg(R+r)sinθ}{{B}^{2}{L}^{2}}$.
(2)恒力F刚推棒EF时棒的加速度为$\frac{F-mgsinθ}{M}$.
(3)棒EF自BD端出发又回到BD端的整个过程中,电阻R上有$\frac{R}{R+r}Fs-$$\frac{RM}{2(R+r)}$[$\frac{Mg(R+r)sinθ}{{B}^{2}{L}^{2}}$]2的电能转化成了内能
点评 本题综合考查了牛顿第二定律、共点力平衡、能量守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
| A. | 第1秒内和第2秒内物体的速度方向相反 | |
| B. | 第2秒内和第3秒内物体的加速度方向相同 | |
| C. | 第2秒末物体的速度和加速度都为零 | |
| D. | 第3秒内物体的速度方向和加速度方向相同 |
 一物体若不受其他外力作用能在一个斜面体上沿斜面减速下滑,可以证明此时斜面受地面向右的摩擦力作用.若沿如图所示方向用力向下推此物体,使物体加速下滑,则斜面受地面的摩擦力是( )
一物体若不受其他外力作用能在一个斜面体上沿斜面减速下滑,可以证明此时斜面受地面向右的摩擦力作用.若沿如图所示方向用力向下推此物体,使物体加速下滑,则斜面受地面的摩擦力是( )| A. | 大小为零 | B. | 方向水平向右 | ||
| C. | 方向水平向左 | D. | 无法判断大小和方向 |
 如图所示,三个相同的灯泡a、b、c和电阻不计线圈L与内阻不计电源连接,下列判断正确的有( )
如图所示,三个相同的灯泡a、b、c和电阻不计线圈L与内阻不计电源连接,下列判断正确的有( )| A. | K闭合的瞬间,b、c两灯一样亮 | |
| B. | K闭合的瞬间,b灯最亮 | |
| C. | K断开的瞬间,a、c两灯立即熄灭 | |
| D. | K断开之后,a、c两灯逐渐变暗且亮度相同 |
| A. | 电磁炉使用时的主要原理是安培分子电流假说 | |
| B. | 电磁炉在使用时线圈的主要作用是产生热量 | |
| C. | 铁质锅底的作用是由于电磁感应产生涡流而发热 | |
| D. | 铁制、铝制、有机玻璃制的锅均可在电磁炉上使用 |
 如图所示是做光电效应实验的装置简图.在抽成真空的玻璃管内,K为阴极(用金属铯制成,发生光电效应的逸出功为1.9eV),A为阳极.在a、b间不接任何电源,用频率为ν(高于铯的极限频率)的单色光照射阴极K,会发现电流表指针有偏转.这时,若在a、b间接入直流电源,a接正极,b接负极,并使a、b间电压从零开始逐渐增大,发现当电压表的示数增大到2.1V时,电流表的示数刚好减小到零.则a、b间未接直流电源时,通过电流表的电流方向为从下向上;从阴极K发出的光电子的最大初动能EK=3.36×10-19J;入射单色光的频率ν=9.65×1014Hz.(h=6.63×10-34J.S)
如图所示是做光电效应实验的装置简图.在抽成真空的玻璃管内,K为阴极(用金属铯制成,发生光电效应的逸出功为1.9eV),A为阳极.在a、b间不接任何电源,用频率为ν(高于铯的极限频率)的单色光照射阴极K,会发现电流表指针有偏转.这时,若在a、b间接入直流电源,a接正极,b接负极,并使a、b间电压从零开始逐渐增大,发现当电压表的示数增大到2.1V时,电流表的示数刚好减小到零.则a、b间未接直流电源时,通过电流表的电流方向为从下向上;从阴极K发出的光电子的最大初动能EK=3.36×10-19J;入射单色光的频率ν=9.65×1014Hz.(h=6.63×10-34J.S)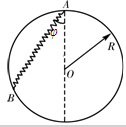 如图所示,一个重为G的小球套在竖直放置的半径为R在光滑圆环上,自然长度为L(L<2R)的轻质弹簧,一端与小球相连,另一端固定在圆环的最高点,小球处于静止状态时,弹簧与竖直方向的夹角φ.
如图所示,一个重为G的小球套在竖直放置的半径为R在光滑圆环上,自然长度为L(L<2R)的轻质弹簧,一端与小球相连,另一端固定在圆环的最高点,小球处于静止状态时,弹簧与竖直方向的夹角φ.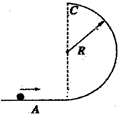 如图所示,半径为R光滑半圆形轨道竖直放置,与水平轨道相接于最低点.质量为m的小球A以某一速度进入轨道内,A通过最高点C时,对管道上部压力为3mg,求A球落地点与C点间的水平距离.
如图所示,半径为R光滑半圆形轨道竖直放置,与水平轨道相接于最低点.质量为m的小球A以某一速度进入轨道内,A通过最高点C时,对管道上部压力为3mg,求A球落地点与C点间的水平距离.