题目内容
16.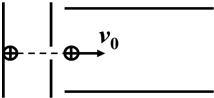 有一质量为m带电荷+q的离子经电压U0加速后,进入两块间距为d,长度为L的平行金属板水平放置,板间电压为U,求:(不计重力)
有一质量为m带电荷+q的离子经电压U0加速后,进入两块间距为d,长度为L的平行金属板水平放置,板间电压为U,求:(不计重力)(1)电荷的在竖直方向位移量y
(2)穿出速度与水平方向的偏转角θ.
分析 设电荷进入偏转电场时速度大小为V0,根据动能定理列式,根据牛顿第二定律求出电荷在偏转电场中的加速度为a,电荷在偏转电场中做类平抛运动,根据平抛运动的基本公式列式,联立方程即可求解.
解答 解:设电荷进入偏转电场时速度大小为V0,根据动能定理得:
$q{U}_{0}=\frac{1}{2}m{{v}_{0}}^{2}$①
电荷在偏转电场中的加速度为a,则
a=$\frac{F}{m}=\frac{qE}{m}=\frac{qU}{md}$②
电荷在偏转电场中运动的时间为t,
则l=v0t ③
偏转位移y=$\frac{1}{2}a{t}^{2}$④
联立①②③④解得:
y=$\frac{U{l}^{2}}{4{U}_{0}d}$,tan$θ=\frac{{v}_{y}}{{v}_{x}}=\frac{qUl}{m{{v}_{0}}^{2}d}=\frac{Ul}{2{U}_{0}d}$
则θ=$arctan\frac{Ul}{2{U}_{0}d}$
答:(1)电荷的在竖直方向位移量y为$\frac{U{l}^{2}}{4{U}_{0}d}$;
(2)穿出速度与水平方向的偏转角θ为$arctan\frac{Ul}{2{U}_{0}d}$.
点评 本题是复合场问题,关键是分析电荷的受力情况和运动情况.在偏转电场中电荷做类平抛运动,采用运动的分解方法研究.

练习册系列答案
相关题目
6. 如图所示,一个导热汽缸竖直放置,汽缸内封闭有一定质量的理想气体,活塞与汽缸壁紧密接触,可沿汽缸壁无摩擦地上下移动.若大气压保持不变,而环境温度缓慢升高,在这个过程中( )
如图所示,一个导热汽缸竖直放置,汽缸内封闭有一定质量的理想气体,活塞与汽缸壁紧密接触,可沿汽缸壁无摩擦地上下移动.若大气压保持不变,而环境温度缓慢升高,在这个过程中( )
 如图所示,一个导热汽缸竖直放置,汽缸内封闭有一定质量的理想气体,活塞与汽缸壁紧密接触,可沿汽缸壁无摩擦地上下移动.若大气压保持不变,而环境温度缓慢升高,在这个过程中( )
如图所示,一个导热汽缸竖直放置,汽缸内封闭有一定质量的理想气体,活塞与汽缸壁紧密接触,可沿汽缸壁无摩擦地上下移动.若大气压保持不变,而环境温度缓慢升高,在这个过程中( )| A. | 汽缸内每个分子的动能都增大 | B. | 封闭气体对外做功 | ||
| C. | 汽缸内单位体积的分子数增多 | D. | 封闭气体放出热量 |
8.以下说法正确的是( )
| A. | 亚里士多德认为,必须有力作用在物体上,物体的运动状态才会改变 | |
| B. | 牛顿用“月-地检验”证实了万有引力定律的正确性 | |
| C. | 卡文迪许测出了引力常量G的数值 | |
| D. | 库伦第一个测出了元电荷的电量 |
5.如图所示是甲、乙两物体做直线运动的s-t图象,由图可知( )
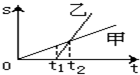

| A. | t1~t2时间内,甲的速度比乙的速度小 | |
| B. | t1~t2时间内,甲的速度比乙的速度大 | |
| C. | t1时刻,两物体的速度大小相等 | |
| D. | 0~t1时间内,甲的位移比乙大 |
6.下列对物体带电现象的叙述正确的是( )
| A. | 经过摩擦使某物体带负电,那么该物体在摩擦过程中产生了额外的电子 | |
| B. | 某物体带电量有可能为3.3×10-19C | |
| C. | 物体所带电量可能很小,但不可能小于元电荷 | |
| D. | 电荷相互中和是电荷完全消失的现象 |
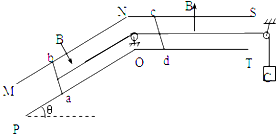 如图所示,相距均为L的光滑倾斜导轨MN、PQ与光滑水平导轨NS、QT连接,水平导轨处在磁感应强度大小为B,方向竖直向上的匀强磁场中.光滑倾斜导轨处在磁感应强度大小也为B,方向垂直于倾斜导轨平面斜向下的匀强磁场中,如图.质量均为m、电阻均为R的金属导体棒ab、cd垂直于导轨分别放在倾斜导轨和水平导轨上,并与导轨接触良好,不计导轨电阻.现用绝缘细线通过定滑轮将金属导体棒ab、cd连接起来.质量为2m的物体C用绝缘细线通过定滑轮与金属导体棒cd连接.细线沿导轨中心线且在导轨平面内,细线及滑轮质量、滑轮摩擦均不计.已知倾斜导轨与水平面的夹角θ=300,重力加速度为g,导轨足够长,导体棒ab始终不离开倾斜导轨,导体棒cd始终不离开水平导轨.物体C由静止释放,当它达到最大速度时下落高度h=$\frac{{m}^{2}g{R}^{2}}{{B}^{4}{L}^{4}}$,试求这一运动过程中:
如图所示,相距均为L的光滑倾斜导轨MN、PQ与光滑水平导轨NS、QT连接,水平导轨处在磁感应强度大小为B,方向竖直向上的匀强磁场中.光滑倾斜导轨处在磁感应强度大小也为B,方向垂直于倾斜导轨平面斜向下的匀强磁场中,如图.质量均为m、电阻均为R的金属导体棒ab、cd垂直于导轨分别放在倾斜导轨和水平导轨上,并与导轨接触良好,不计导轨电阻.现用绝缘细线通过定滑轮将金属导体棒ab、cd连接起来.质量为2m的物体C用绝缘细线通过定滑轮与金属导体棒cd连接.细线沿导轨中心线且在导轨平面内,细线及滑轮质量、滑轮摩擦均不计.已知倾斜导轨与水平面的夹角θ=300,重力加速度为g,导轨足够长,导体棒ab始终不离开倾斜导轨,导体棒cd始终不离开水平导轨.物体C由静止释放,当它达到最大速度时下落高度h=$\frac{{m}^{2}g{R}^{2}}{{B}^{4}{L}^{4}}$,试求这一运动过程中: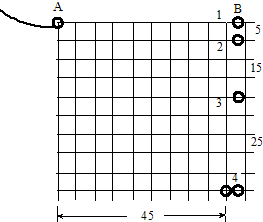 如图所示,是利用闪光照相研究平抛运动的示意图.小球A由斜槽滚下,从桌边缘水平抛出,当它恰好离开桌边缘时,小球B也同时下落,闪光周期为0.1s的闪光器拍摄的照片中B球有四个像,像间距离已在图中标出,单位为cm,两球恰在位置4相碰,则A球离开桌面时的速度大小为1.5m/s.
如图所示,是利用闪光照相研究平抛运动的示意图.小球A由斜槽滚下,从桌边缘水平抛出,当它恰好离开桌边缘时,小球B也同时下落,闪光周期为0.1s的闪光器拍摄的照片中B球有四个像,像间距离已在图中标出,单位为cm,两球恰在位置4相碰,则A球离开桌面时的速度大小为1.5m/s.