题目内容
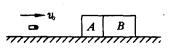
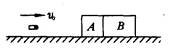
 如图所示,有两个物体A,B,紧靠着放在光滑水平桌面上,A的质量为2kg,B的质量为3kg.有一颗质量为100g的子弹以800m/s的水平速度射入A,经过0.01s又射入物体B,最后停在B中,A对子弹的阻力为3×103N,(小数点后取一位有效数字).
如图所示,有两个物体A,B,紧靠着放在光滑水平桌面上,A的质量为2kg,B的质量为3kg.有一颗质量为100g的子弹以800m/s的水平速度射入A,经过0.01s又射入物体B,最后停在B中,A对子弹的阻力为3×103N,(小数点后取一位有效数字).求(1)A、B最终的速度;
(2)若不考虑对外散热,则系统内能增加多少?
分析:(1)本题知道子弹所受的阻力大小和时间,对于子弹击穿A的过程,运用动量定理求出A、B获得的速度,子弹射入B后,A、B分离,A做匀速直线运动,速度不变,再对系统,根据动量守恒定律列式求B的最终速度.
(2)整个过程,系统的机械能减少,转化为内能,根据能量守恒求解系统内能增加.
(2)整个过程,系统的机械能减少,转化为内能,根据能量守恒求解系统内能增加.
解答:解:(1)子弹击穿A时,对A、B由动量定理:
ft=(mA+mB)vA,
解得,vA=
=6m/s
在整个过程中对A、B及子弹系统,由动量守恒得:mv0=mAvA+(mB+m)vB,
故 vB=22m/s
(2)整个过程,系统的机械能减少,转化为内能,根据能量守恒得
△E=
m
-
mA
-
(mB+mC)
=31213.8J
答:
(1)A、B最终的速度是22m/s;
(2)若不考虑对外散热,则系统内能增加是31213.8J.
ft=(mA+mB)vA,
解得,vA=
| ft |
| mA+mB |
在整个过程中对A、B及子弹系统,由动量守恒得:mv0=mAvA+(mB+m)vB,
故 vB=22m/s
(2)整个过程,系统的机械能减少,转化为内能,根据能量守恒得
△E=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
答:
(1)A、B最终的速度是22m/s;
(2)若不考虑对外散热,则系统内能增加是31213.8J.
点评:本题关键灵活地选择研究对象和研究过程,运用动量定理、动量守恒定律和能量守恒列式求解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
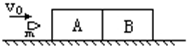 如图所示,有两个物体A,B,紧靠着放在光滑水平桌面上,A的质量为2kg,B的质量为3kg.有一颗质量为100g的子弹以800m/s的水平速度射入A,经过0.01s又射入物体B,最后停在B中,A对子弹的阻力为3×103N,求A,B最终的速度.
如图所示,有两个物体A,B,紧靠着放在光滑水平桌面上,A的质量为2kg,B的质量为3kg.有一颗质量为100g的子弹以800m/s的水平速度射入A,经过0.01s又射入物体B,最后停在B中,A对子弹的阻力为3×103N,求A,B最终的速度.