题目内容
 某学校物理兴趣小组用空心透明光滑塑料管制作了如图所示的“06”造型,固定在竖直平面内,底端与水平地面相切.两个圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C是轨道上的两点,B是右侧“6”字型的最低点,C点的左侧“0”字型上与圆心等高的一点.D为水平出口,其高度与圆最高点相同.已知A比D高R,当地的重力加速度为g,不计一切阻力.求:
某学校物理兴趣小组用空心透明光滑塑料管制作了如图所示的“06”造型,固定在竖直平面内,底端与水平地面相切.两个圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C是轨道上的两点,B是右侧“6”字型的最低点,C点的左侧“0”字型上与圆心等高的一点.D为水平出口,其高度与圆最高点相同.已知A比D高R,当地的重力加速度为g,不计一切阻力.求:(1)小物体从D点抛出后的水平射程;
(2)小球经过B点时对管道的压力大小;
(3)小球经过C点时的加速度大小.
分析:(1)让小球在竖直放置的空心透明光滑塑料管运动,利用牛顿第二定律与圆周运动的向心力公式,可求出某点的受力情况.同时运用动能定理,可找出某两点的速度与这两点的高度关系.小球从高于D点的A点静止释放,由于光滑,则由动能定理,可得出小球从E点射出速度,再由平抛运动规律可求出水平射程.
(2)当小球到达最低B点,由速度结合牛顿第二定律可得出小球的受力情况.
(3)小球在C点时,仅仅受到重力与支持力作用,因此可以分别求出切向方向与法向方向的加速度,再进行合成,从而求出加速度大小.
(2)当小球到达最低B点,由速度结合牛顿第二定律可得出小球的受力情况.
(3)小球在C点时,仅仅受到重力与支持力作用,因此可以分别求出切向方向与法向方向的加速度,再进行合成,从而求出加速度大小.
解答:解:(1)对小球从A到D的过程用动能定理得:mgR=
m
小球从D射出到地面做平抛运动,
水平方向:x=vDt
竖直方向:2R=
gt2
由以上三式得:x=2
R
(2)对小球从A到B的过程用动能定理
得:mg?3R=
m
根据B点的向心力公式有:FB-mg=
解得:FB=7mg
(3)对小球从A到C的过程用动能定理
可得:mg?2R=
m
小球在C点的水平方向加速度为向心加速度,即a1=
小球在C点的竖直方向的加速度为:a2=g
所以小球在C点的合加速度为:aC=
由以上式子可解得:aC=
g
答:(1)小物体从D点抛出后的水平射程2
R.
(2)小球经过B点时对管道的压力大小7mg.
(3)小球经过C点时的加速度大小
g.
| 1 |
| 2 |
| v | 2 D |
小球从D射出到地面做平抛运动,
水平方向:x=vDt
竖直方向:2R=
| 1 |
| 2 |
由以上三式得:x=2
| 2 |
(2)对小球从A到B的过程用动能定理
得:mg?3R=
| 1 |
| 2 |
| v | 2 B |
根据B点的向心力公式有:FB-mg=
m
| ||
| R |
解得:FB=7mg
(3)对小球从A到C的过程用动能定理
可得:mg?2R=
| 1 |
| 2 |
| v | 2 C |
小球在C点的水平方向加速度为向心加速度,即a1=
| ||
| R |
小球在C点的竖直方向的加速度为:a2=g
所以小球在C点的合加速度为:aC=
|
由以上式子可解得:aC=
| 17 |
答:(1)小物体从D点抛出后的水平射程2
| 2 |
(2)小球经过B点时对管道的压力大小7mg.
(3)小球经过C点时的加速度大小
| 17 |
点评:本题考查圆周运动的向心力、牛顿第二定律、平抛运动规律与动能定理,及平行四边形定则.同时对小球进行受力分析与运动分析小球.值得注意是,当小球在C点的受力分析,重力产生的切向加速度,而支持力则产生的法向加速度(向心加速度).

练习册系列答案
相关题目
 某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型,两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,不计空气阻力和因碰撞而损失的机械能,则在整个运动过程中( )
某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型,两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,不计空气阻力和因碰撞而损失的机械能,则在整个运动过程中( )| A、如果是不光滑小球,小球一定不能从E点射出 | B、如果是光滑小球,在D点处,塑料管的左侧对小球的压力为4mg | C、如果是光滑小球,且能到达C点,此处塑料管对小球的弹力小于mg | D、如果是不光滑小球,小球不可能停在B点 |
 (2011?湖南一模)“六十甲子”是古人发明用来计时的方法,也是一种表示自然界五行之气循环流转的直观表示法.某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型.两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,则小球在整个运动过程中,下列说法正确的是( )
(2011?湖南一模)“六十甲子”是古人发明用来计时的方法,也是一种表示自然界五行之气循环流转的直观表示法.某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型.两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,则小球在整个运动过程中,下列说法正确的是( )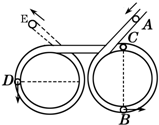 某学校物理兴趣小组用空心透明塑料管制作了如图所示装置.两个“0”字型的半径均为R.让一质量为m、直径略小于管径的光滑小球从入口A处射入,依次经过图中的B、C、D三点,最后从E点飞出.已知BC是“0”字型的一条直径,D点是该造型最左侧的一点,当地的重力加速度为g,不计一切阻力,则小球在整个运动过程中( )
某学校物理兴趣小组用空心透明塑料管制作了如图所示装置.两个“0”字型的半径均为R.让一质量为m、直径略小于管径的光滑小球从入口A处射入,依次经过图中的B、C、D三点,最后从E点飞出.已知BC是“0”字型的一条直径,D点是该造型最左侧的一点,当地的重力加速度为g,不计一切阻力,则小球在整个运动过程中( ) “六十甲子”是古人发明用来计时的方法,也是一种表示自然界五行之气循环流转的直观表示法.某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型.两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,则小球在整个运动过程中,下列说法错误的是( )
“六十甲子”是古人发明用来计时的方法,也是一种表示自然界五行之气循环流转的直观表示法.某学校物理兴趣小组用空心透明粗糙塑料管制作了如图所示的竖直“60”造型.两个“0”字型圆的半径均为R.让一质量为m、直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度低于入口A.已知BC是“0”字型的一条竖直方向的直径,D点是左侧“0”字型上的一点,与圆心等高,A比C高R,当地的重力加速度为g,则小球在整个运动过程中,下列说法错误的是( )