题目内容
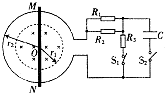 (2013?南宁三模)如图所示,半径为r1,的圆形区域内有匀强磁场,磁场的磁感应强度大小为B0、方向 垂直纸面向里,半径为r2的金属圆环右侧开口处与右侧电路相连,已知圆环电阻为R,电阻R1=R2=R3=R,电容器的电容为C,圆环圆心O与磁场圆心重合,一金属棒MN与金属环接触良好,不计棒与导线的电阻,电键S1处于闭合状态、电键S2处于断开状态.
(2013?南宁三模)如图所示,半径为r1,的圆形区域内有匀强磁场,磁场的磁感应强度大小为B0、方向 垂直纸面向里,半径为r2的金属圆环右侧开口处与右侧电路相连,已知圆环电阻为R,电阻R1=R2=R3=R,电容器的电容为C,圆环圆心O与磁场圆心重合,一金属棒MN与金属环接触良好,不计棒与导线的电阻,电键S1处于闭合状态、电键S2处于断开状态.(1)若棒MN以速度v0沿环向右匀速滑动,求棒滑过圆环直径的瞬间产生的电动势和流过R1的电流;
(2)撤去棒MN后,闭合电键S2,调节磁场,使磁感应强度B的变化率n,n为常数,求电路稳定时电阻R3在t0时间内产生的焦耳热;
(3)在(2)问情形下,求断开电键S1后流过电阻R2的电量.
分析:(1)根据棒切割磁感线,从而产生感应电动势,并由欧姆定律,即可求解;
(2)由法拉第电磁感应定律求出线圈中产生的感应电动势,由欧姆定律求出感应电流的大小,由楞次定律判断出感应电流的方向.由公式q=It求出通过电阻R1上的电量q,由焦耳定律求出电阻R1上产生的热量.
(3)断开电键S1前后电容器两极板上的电压发生变化,电容器上电量的变化对于流过电阻R1和R2的电量的和.
(2)由法拉第电磁感应定律求出线圈中产生的感应电动势,由欧姆定律求出感应电流的大小,由楞次定律判断出感应电流的方向.由公式q=It求出通过电阻R1上的电量q,由焦耳定律求出电阻R1上产生的热量.
(3)断开电键S1前后电容器两极板上的电压发生变化,电容器上电量的变化对于流过电阻R1和R2的电量的和.
解答:解:(1)由法拉第电磁感应定律,则有:E=B0(2r1)v0=2B0r1v0,
MN右侧的电路中,圆环部分的电阻是圆环电阻为R的一半(
),R1与R2并联的电阻是
,所以MN右侧的总电阻是:
+
+R=2R.
应用导体棒的电阻不计,所以电路的路端电压等于电源的电动势.根据欧姆定律,解得:I=
=
,
由于R1与R2相等,所以流过R1上的电流:I1=
I=
(2)由题意可知,0至t时间内 由法拉第电磁感应定律有:
E′=
=
S=k?π
由闭合电路欧姆定律有:
I′=
=
电阻R3在t0时间内产生的焦耳热:
Q=I′2R?t0=
(3)S1闭合时,电容器两端的电压等于R3两端的电压,
U3=I′?R=
S1断开后,电容器两端的电压等于电源的电动势E′,
电容器上电量的改变为:△Q=C?△U=C(E′-U3)=
由于R1与R2相等,所以两个两个电阻上的电量相等,流过R1上的电量:q=
=
.
答:(1)棒滑过圆环直径的瞬间产生的电动势2B0r1v0,流过R1的电流为
;
(2)电路稳定时电阻R3在t0时间内产生的焦耳热为
;
(3)在(2)问情形下,求断开电键S1后流过电阻R2的电量为
.
MN右侧的电路中,圆环部分的电阻是圆环电阻为R的一半(
| R |
| 2 |
| R |
| 2 |
| R |
| 2 |
| R |
| 2 |
应用导体棒的电阻不计,所以电路的路端电压等于电源的电动势.根据欧姆定律,解得:I=
| E |
| 2R |
| B0r1v0 |
| R |
由于R1与R2相等,所以流过R1上的电流:I1=
| 1 |
| 2 |
| B0r1v0 |
| 2R |
(2)由题意可知,0至t时间内 由法拉第电磁感应定律有:
E′=
| △Φ |
| △t |
| △B |
| △t |
| r | 2 1 |
由闭合电路欧姆定律有:
I′=
| E′ | ||
R+
|
2kπ
| ||
| 5R |
电阻R3在t0时间内产生的焦耳热:
Q=I′2R?t0=
4k2π2
| ||
| 25R |
(3)S1闭合时,电容器两端的电压等于R3两端的电压,
U3=I′?R=
2kπ
| ||
| 5 |
S1断开后,电容器两端的电压等于电源的电动势E′,
电容器上电量的改变为:△Q=C?△U=C(E′-U3)=
3kπC
| ||
| 5R |
由于R1与R2相等,所以两个两个电阻上的电量相等,流过R1上的电量:q=
| Q |
| 2 |
3kπC
| ||
| 10R |
答:(1)棒滑过圆环直径的瞬间产生的电动势2B0r1v0,流过R1的电流为
| B0r1v0 |
| 2R |
(2)电路稳定时电阻R3在t0时间内产生的焦耳热为
4k2π2
| ||
| 25R |
(3)在(2)问情形下,求断开电键S1后流过电阻R2的电量为
3kπC
| ||
| 10R |
点评:本题是法拉第电磁感应定律、欧姆定律、焦耳定律的综合应用,应用法拉第定律时要注意s是有效面积,并不等于线圈的面积.

练习册系列答案
相关题目
 (2013?南宁三模)(改、2010年北京101中学调研)当用具有1.87eV能量的光子照射n=3激发态的氢原子时( )
(2013?南宁三模)(改、2010年北京101中学调研)当用具有1.87eV能量的光子照射n=3激发态的氢原子时( ) (2013?南宁三模)如图,OO′是半圆柱形玻璃的对称轴在纸面上的投影.在圆内有两细束与OO′平行且等距的单色光A和B,从玻璃砖射出后相交于OO′下方的P点,由此可以得出的正确结论是( )
(2013?南宁三模)如图,OO′是半圆柱形玻璃的对称轴在纸面上的投影.在圆内有两细束与OO′平行且等距的单色光A和B,从玻璃砖射出后相交于OO′下方的P点,由此可以得出的正确结论是( ) (2013?南宁三模)2008年9月我国成功发射了“神州七号”载人飞船.为了观察“神舟七号”的运行和宇航员仓外活动情况,飞船利用弹射装置发射一颗“伴星”.伴星经调整后,和“神舟七号”一样绕地球做匀速圆周运动,但比“神舟七号”离地面稍高一些,如图所示,那么( )
(2013?南宁三模)2008年9月我国成功发射了“神州七号”载人飞船.为了观察“神舟七号”的运行和宇航员仓外活动情况,飞船利用弹射装置发射一颗“伴星”.伴星经调整后,和“神舟七号”一样绕地球做匀速圆周运动,但比“神舟七号”离地面稍高一些,如图所示,那么( ) (2013?南宁三模)一只矩形线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,穿过线圈的磁通量随时间变化的图象如图甲所示,则下列说法中的正确的是( )
(2013?南宁三模)一只矩形线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,穿过线圈的磁通量随时间变化的图象如图甲所示,则下列说法中的正确的是( )