题目内容
1879年美国物理学家霍尔在研究载流导体在磁场中受力情况时,发现了一种新的电磁效应:将导体置于磁场中,并沿垂直磁场方向通入电流,则在导体中垂直于电流和磁场的方向会产生一个横向电势差,这种现象后来被称为霍尔效应,这个横向的电势差称为霍尔电势差。
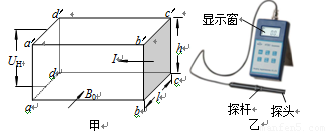
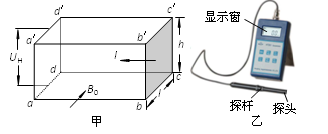
1.如图甲所示,某长方体导体abcda′b′c′d′的高度为h、宽度为l,其中的载流子为自由电子,其电荷量为e,处在与ab b′a′面垂直的匀强磁场中,磁感应强度为B0。在导体中通有垂直于bcc′b′面的电流,若测得通过导体的恒定电流为I,横向霍尔电势差为UH,求此导体中单位体积内自由电子的个数。
2.对于某种确定的导体材料,其单位体积内的载流子数目n和载流子所带电荷量q均为定值,人们将H=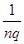 定义为该导体材料的霍尔系数。利用霍尔系数H已知的材料可以制成测量磁感应强度的探头,有些探头的体积很小,其正对横截面(相当于图14甲中的ab b′a′面)的面积可以在0.1cm2以下,因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器,其中的探头装在探杆的前端,且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小I,又可以监测出探头所产生的霍尔电势差UH,并自动计算出探头所测位置磁场的磁感应强度的大小,且显示在仪器的显示窗内。
定义为该导体材料的霍尔系数。利用霍尔系数H已知的材料可以制成测量磁感应强度的探头,有些探头的体积很小,其正对横截面(相当于图14甲中的ab b′a′面)的面积可以在0.1cm2以下,因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器,其中的探头装在探杆的前端,且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小I,又可以监测出探头所产生的霍尔电势差UH,并自动计算出探头所测位置磁场的磁感应强度的大小,且显示在仪器的显示窗内。
①在利用上述仪器测量磁感应强度的过程中,对探杆的放置方位有何要求;
②要计算出所测位置磁场的磁感应强度,除了要知道H、I、UH外,还需要知道哪个物理量,并用字母表示。推导出用上述这些物理量表示所测位置磁感应强度大小的表达式。
1.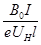
2.见解析
【解析】(1)设单位体积内的自由电子数为n,自由电子定向移动的速率为v,
则有 I=nehlv……………………………………………………………………(1分)
当形成恒定电流时,自由电子所受电场力与洛仑兹力相等,因此有
evB0=eUH/h………………………………………………………………………(2分)
解得n=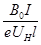 …………………………………………………………………(1分)
…………………………………………………………………(1分)
(2)①应调整探杆的放置方位(或调整探头的方位),使霍尔电势差达到最大(或使探杆与磁场方向平行;探头的正对横截面与磁场方向垂直;ab b′a′面与磁场方向垂直)…………………………………………………………………………………………(3分)
②设探头中的载流子所带电荷量为q,根据上述分析可知,探头处于磁感应强度为B的磁场中,当通有恒定电流I,产生最大稳定霍尔电压UH时,有 qvB=qUH/h…………(1分)
又因 I=nqhlv和H=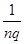
联立可解得 B=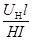 ……………………………………………………………(1分)
……………………………………………………………(1分)
所以,还需要知道探头沿磁场方向的宽度l……………………………………(1分)

 阅读快车系列答案
阅读快车系列答案
 向霍尔电势差为UH,求此导体中单位体积内自由电子的个数。
向霍尔电势差为UH,求此导体中单位体积内自由电子的个数。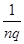 定义为该导体材料的霍尔系数。利用霍尔系数H已知的材料可以制成测量磁感应强度的探头,有些探头的体积很小,其正对横截面(相当于图14甲中的ab b′a′面)的面积可以在0.1cm2以下,因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器,其中的探头装在探杆的前端,且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小I,又可以监测出探头所产生的霍尔电势差UH,并自动计算出探头所测位置磁场的磁感应强度的大小,且显示在仪器的显示窗内。
定义为该导体材料的霍尔系数。利用霍尔系数H已知的材料可以制成测量磁感应强度的探头,有些探头的体积很小,其正对横截面(相当于图14甲中的ab b′a′面)的面积可以在0.1cm2以下,因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器,其中的探头装在探杆的前端,且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小I,又可以监测出探头所产生的霍尔电势差UH,并自动计算出探头所测位置磁场的磁感应强度的大小,且显示在仪器的显示窗内。