题目内容
12. 如图所示,在两条平行的虚线内存在着宽度为L、场强为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:
如图所示,在两条平行的虚线内存在着宽度为L、场强为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:(1)粒子从射入到打到屏上所用的时间;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值;
(3)粒子打到屏上的点P到O点的距离.
分析 (1)带电粒子垂直射入电场,只受电场力作用而做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速运动,由L=v0t求解时间t.
(2)根据牛顿第二定律求出加速度.研究竖直方向的运动情况,由速度公式vy=at求出粒子刚射出电场时竖直分速度,由tanα=$\frac{{v}_{y}}{{v}_{0}}$求出tanα.
(3)由位移公式y=$\frac{1}{2}$at2求出粒子刚射出电场时偏转的距离y.带电粒子离开电场后做匀速直线运动,偏转的距离Ltanα,两个偏转之和即为粒子打到屏上的点P到O点的距离Y.
解答 解:(1)粒子在垂直于电场线的方向上做匀速直线运动,
则粒子打到荧光屏上的时间:t′=$\frac{2L}{{v}_{0}}$.
(2)设粒子射出电场时沿平行电场线方向的速度为vy,
根据牛顿第二定律,粒子在电场中的加速度为:a=$\frac{qE}{m}$,
所以vy=at=a$\frac{L}{{v}_{0}}$=$\frac{qEL}{m{v}_{0}}$,
粒子刚射出电场时的速度方向与初速度方向间夹角的正切值为:tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{qEL}{m{v}_{0}^{2}}$.
(3)设粒子在电场中的偏转距离为y,则y=$\frac{1}{2}$at2=$\frac{1}{2}$•$\frac{qEL}{m{v}_{0}}$t2
又Y=y+Ltanα,解得:Y=$\frac{3qE{L}^{2}}{2m{v}_{0}^{2}}$;
答:(1)粒子从射入到打到屏上所用的时间是$\frac{2L}{{v}_{0}}$;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα为$\frac{qEL}{m{v}_{0}^{2}}$;
(3)粒子打到屏上的点P到O点的距离Y为$\frac{3qE{L}^{2}}{2m{v}_{0}^{2}}$.
点评 本题中带电粒子先做类平抛运动后做匀速直线运动,运用运动的分解研究类平抛运动,根据几何知识求解Y.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 通过导线横截面的电量越多,电流强度越大 | |
| B. | 电流强度的单位是安培,此单位不是国际单位制中的基本单位 | |
| C. | 单位时间内,通过导体横截面的电量越多,导体中的电流强度越大 | |
| D. | 因为电流有方向,所以电流强度是矢量 |
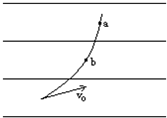 图中的平行直线为匀强电场的电场线,曲线为电子在该电场中的运动轨迹,a,b是轨迹上的两点,则下列正确说法的是( )
图中的平行直线为匀强电场的电场线,曲线为电子在该电场中的运动轨迹,a,b是轨迹上的两点,则下列正确说法的是( )| A. | 电场线的方向水平向右 | |
| B. | 电子在b点的电势能大于在a点的电势能 | |
| C. | 电子在b点的加速度大于在a点的加速度 | |
| D. | a点的电势高于b点的电势 |

| A. | 在t=1.5s时,穿过线圈P的磁通量最大,感应电流最大 | |
| B. | 在t=1.5s时,穿过线圈P的磁通量最大,此时FT=0.5mg | |
| C. | 在t=3s时,穿过线圈P的磁通量的变化率为零 | |
| D. | 在0~3s内,线圈P受到的安培力先变大再变小 |
 空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H.则以下判断中正确的是( )
空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H.则以下判断中正确的是( )| A. | 若v2>v1,则电场力一定做正功 | |
| B. | A、B两点间的电势差U=$\frac{m({{v}_{2}}^{2}-{{v}_{1}}^{2})}{2q}$ | |
| C. | 小球由A点运动至B点,电场力做的功W=$\frac{m{{v}_{2}}^{2}}{2}$-$\frac{m{{v}_{1}}^{2}}{2}$-mgH | |
| D. | 小球运动到B点时所受重力的瞬时功率P=mgv2 |
 如图所示的电路中,已知电阻R1:R2=1:3.如果甲、乙两表均为电压表,当开关S闭合时,此时,两表的示数之比U甲:U乙=1:4;如果甲、乙两表均为电流表,当开关S断开时,两表的示数之比I甲:I乙=4:3.
如图所示的电路中,已知电阻R1:R2=1:3.如果甲、乙两表均为电压表,当开关S闭合时,此时,两表的示数之比U甲:U乙=1:4;如果甲、乙两表均为电流表,当开关S断开时,两表的示数之比I甲:I乙=4:3. 如图是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道.表演者骑着摩托车在圆轨道内做圆周运动.已知人和摩托车的总质量为m,人以v1=$\sqrt{2gR}$的速度过轨道最高点B,并以v2=$\sqrt{3}$v1的速度过最低点A.求在A、B两点,轨道对摩托车的压力大小相差多少?(g为重力加速度)
如图是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道.表演者骑着摩托车在圆轨道内做圆周运动.已知人和摩托车的总质量为m,人以v1=$\sqrt{2gR}$的速度过轨道最高点B,并以v2=$\sqrt{3}$v1的速度过最低点A.求在A、B两点,轨道对摩托车的压力大小相差多少?(g为重力加速度)